⇦Chinese Physics Letters, 2019, Vol. 36, No. 9, Article code 097502 Magnetic and Magnetocaloric Properties of Polycrystalline and Oriented Mn$_{2-\delta}$Sn * Kun Li (李昆)1,2, Fanggui Wang (王芳贵)1,2, Youfang Lai (赖有方)1,2, Mingzhu Xue (薛明珠)1,2, Xin Li (李鑫)1,2, Jinbo Yang (杨金波)1,2,3, Changsheng Wang (王常生)1,2, Jingzhi Han (韩景智)1,2, Shunquan Liu (刘顺荃)1,2, Wenyun Yang (杨文云)1,2, Yingchang Yang (杨应昌)1,2, Honglin Du (杜红林)1,2** Affiliations 1School of Physics, Peking University, Beijing 100871 2Beijing Key Laboratory for Magnetoelectric Materials and Devices, Beijing 100871 3Collaborative Innovation Center of Quantum Matter, Beijing 100871 Received 5 May 2019, online 23 August 2019 *Supported by the National Natural Science Foundation of China under Grant Nos 11675006, 51731001 and 11805006, and the National Key Research and Development Program of China under Grant Nos 2017YFA0206303, 2016YFB0700901 and 2017YFA0403701.
**Corresponding author. Email: duhonglin@pku.edu.cn Citation Text: Li K, Wang F G, Lai Y F, Xue M Z and Li X et al 2019 Chin. Phys. Lett. 36 097502    Abstract Mn-based Heusler alloys have attracted significant research attention as half-metallic materials because of their giant magnetocrystalline anisotropy and magnetocaloric properties. We investigate the crystal structure and magnetic properties of polycrystalline, [101]-oriented, and [100]-oriented Mn$_{2-\delta}$Sn prepared separately by arc melting, the Bridgeman method, and the flux method. All of these compounds crystallize in a Ni$_{2}$In-type structure. In the Mn$_{2-\delta}$Sn lattice, Mn atoms occupy all of the 2$a$ and a fraction of the 2$d$ sites. Site disorder exists between Mn and Sn atoms in the 2$c$ sites. In addition, these compounds undergo a re-entrant spin-glass-like transition at low temperatures, which is caused by frustration and randomness within the spin system. The magnetic properties of these systems depend on the crystal directions, which means that the magnetic interactions differ significantly along different directions. Furthermore, these materials exhibit a giant magnetocaloric effect near the Curie temperature. The largest value of maximum of magnetic entropy change ($-\Delta S_{\rm M})$ occurs perpendicular to the [100] direction. Specifically, at 252 K, maximum $-\Delta S_{\rm M}$ is 2.91 and 3.64 J$\cdot$kg$^{-1}$K$^{-1}$ for a magnetic field of 5 and 7 T, respectively. The working temperature span over 80 K and the relative cooling power reaches 302 J/kg for a magnetic field of 7 T, which makes the Mn$_{2-\delta}$Sn compound a promising candidate for a magnetic refrigerator. DOI:10.1088/0256-307X/36/9/097502 PACS:75.30.Gw, 75.30.Sg © 2019 Chinese Physics Society Article Text In recent years, considerable attention has been paid to 'half-metallic' materials with complete spin polarization at the Fermi level ($E_{\rm F}$).[1–7] The Heusler alloys constitute a large family of half-metallic materials,[1,8–11] which may be divided into full-Heusler and half-Heusler alloys according to the number of atoms in the unit cell. The chemical formulas for these compounds are $A_{2}BC$ and $ABC$, respectively, where $A$ and $B$ are transition-metal elements and $C$ is a main-group element. In the half-Heusler alloys, their unit cell can be regarded as one $A$ atom is replaced by a vacant site in the full-Heusler unit cell.[4,8] As half-metallic Heusler alloys, Mn-based alloys with the non-cubic crystal structure have attracted significant attention. Some of these alloys have large magnetocrystalline anisotropy and high Curie temperature above room temperature,[12,13] while some have competing ferro-and-antiferromagnetic interactions between transition-metal moments located at different lattice sites.[14–16] In addition, because of their magnetocaloric effects, Mn-based alloys have also been extensively studied in the field of magnetic refrigeration. Due to a series of problems in traditional refrigeration technology (e.g., environmental pollution), many studies have focused on magnetic refrigeration, which is an emerging environmentally friendly refrigeration technology.[17–20] In the study of the magnetocaloric effect of Mn-based alloys, there were some studies on Mn$_{2-\delta}$Sn doped materials. Few previous reports have focused on the magnetic and magnetocaloric properties of Mn$_{2-\delta}$Sn. To better understand these materials, we systematically study the magnetic properties and magnetic interactions of single-phase polycrystalline, [101]-oriented and [100]-oriented samples of Mn$_{2-\delta}$Sn alloys. We prepared a polycrystalline sample of Mn$_{2-\delta}$Sn with a nominal composition of Mn$_{1.9}$Sn by arc melting under an Ar atmosphere. The purity of the constituent elements exceeded 99%, and the sample was vacuum annealed at 1123 K for three days. The [101]-oriented and [100]-oriented Mn$_{2-\delta}$Sn samples were grown by the Bridgeman method and the flux method, respectively. The nominal composition of the polycrystalline sample, which was also the raw material of the Bridgeman method, was Mn$_{1.9}$Sn while the ratio of Mn:Sn in the flux method was 1:2 (Sn is the flux). Room-temperature x-ray diffraction measurements were carried using an X'pert Pro MPD diffractometer (Cu $K_{\alpha}$ radiation, $\lambda =1.54187$ Å) and confirmed that all the samples were single phase. The magnetization measurements were made by a conventional physical property measurement system (PPMS-9,2–350 K). Although Mn$_{2-\delta}$Sn is predicted to form either a cubic or hexagonal crystal structure, only the hexagonal $B8_{2}$ phase (a Ni$_{2}$In-type structure) with space group $p63/mmc$ ($a=4.37$–4.40 Å, $c$=5.47–5.53 Å)[14,21–25] has been prepared experimentally.[26,27]
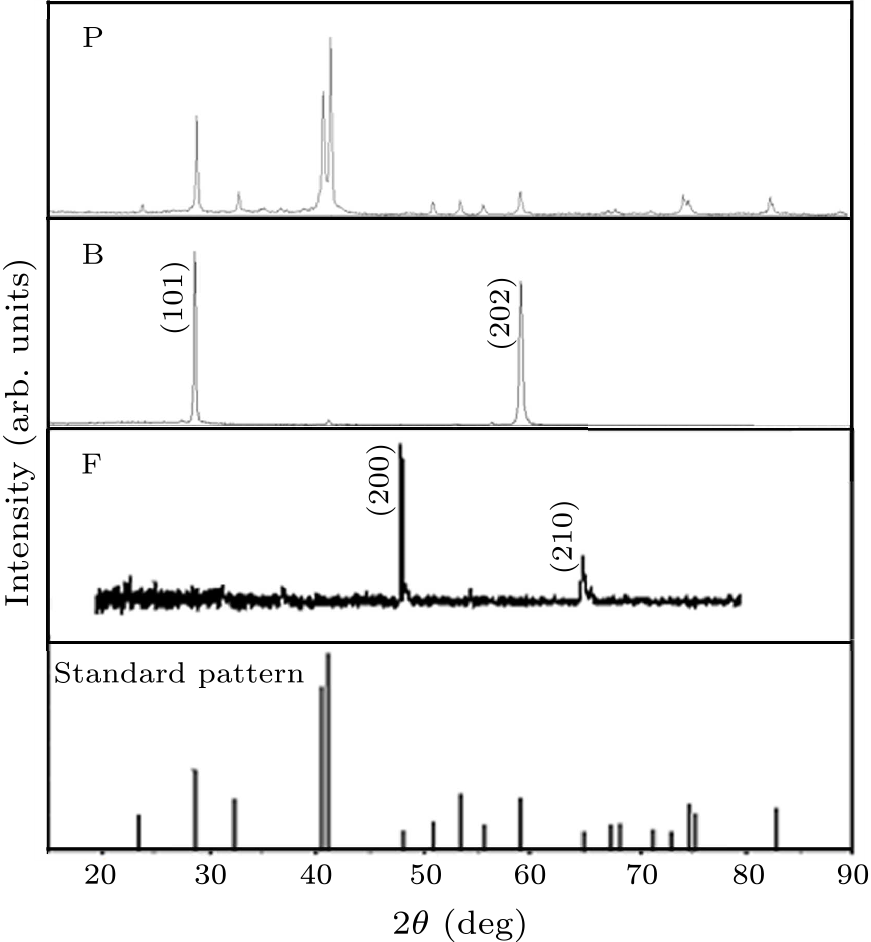
cpl-36-9-097502-fig1.png
Fig. 1. X-ray diffraction patterns of P, B and F samples and of a standard sample.
The notations P, B and F indicate the samples prepared by arc-melting, the Bridgeman method and the flux method, respectively (the size of B is $2\times 2\times1$ mm$^{3}$ and the size of F is $3\times 1\times1$ mm$^{3}$). Figure 1 shows the x-ray diffraction patterns of the three different samples. The diffraction pattern produced by sample P can be indexed as a single phase of hexagonal Ni$_{2}$In-type structure. Rietveld refinement shows that, in the Mn$_{2-\delta}$Sn lattice, Mn atoms occupy all Wyckoff 2$a$ sites and a fraction of the 2$d$ sites, and the 2$c$ sites are randomly occupied by a small amount of Mn and all the Sn atoms. These results are consistent with those of the previous studies.[14,21–25] The refined lattice parameters for sample P are $a$=4.395(3) Å and $c$=5.520(1) Å. By indexing the standard pattern, we find that (as expected) sample B grew along the [101] direction, which is parallel to the pulling direction of the Bridgman method. To investigate the magnetic properties of Mn$_{2-\delta}$Sn in the [100] direction, we selected sample F, which grew primarily along the [100] direction (and slightly along the [210] direction), from hundreds of crystals. Since the (210) peak is very weak, we consider sample F to be oriented in the [100] direction. Figure 2 shows the thermomagnetic curves (5–300 K in a field of 50 Oe) under zero-field-cooled (ZFC) and field-cooled (FC) conditions. In addition, sample B (F) was measured with an applied magnetic field parallel (denoted by Bp (Fp)) and perpendicular (denoted by Bv (Fv)) with respect to the [101] ([100]) direction, respectively.
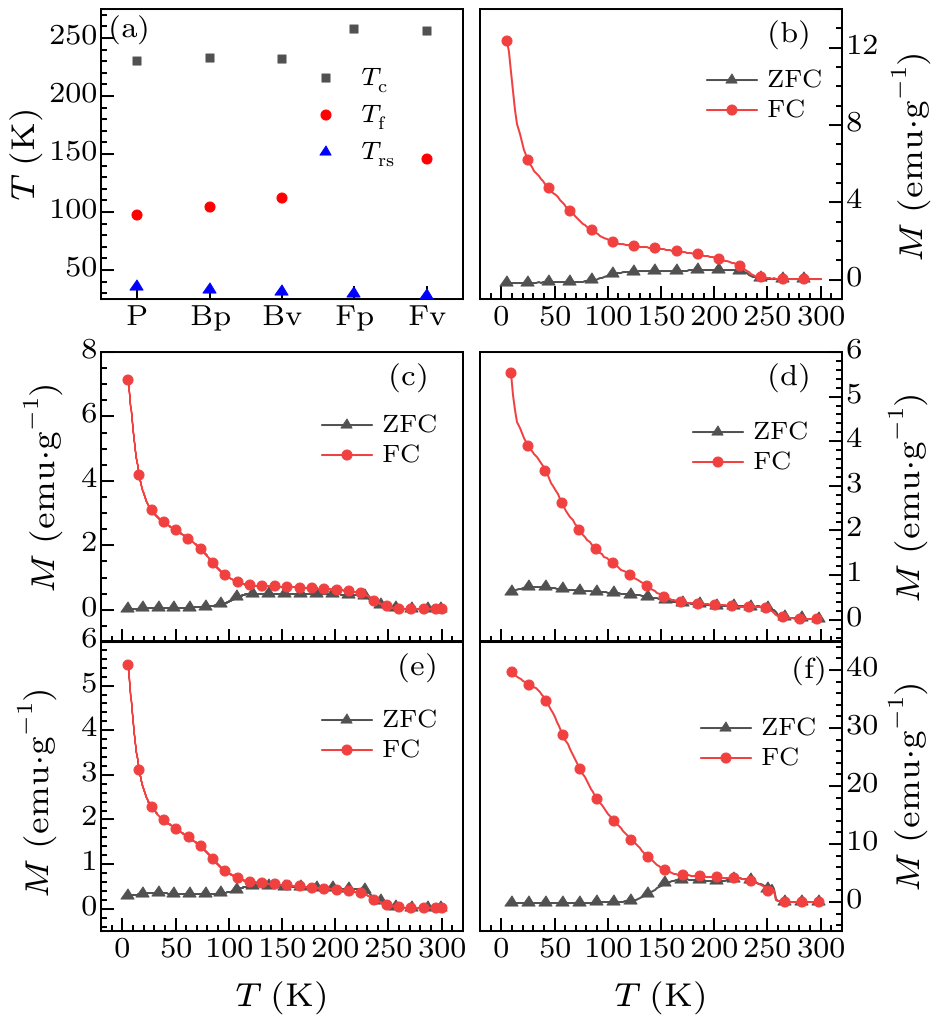
cpl-36-9-097502-fig2.png
Fig. 2. (a) Magnetic transition temperature for different samples. Here $T_{\rm C}$ is the Curie temperature, $T_{\rm f}$ is the freezing temperature, and $T_{\rm rs}$ is the spin-reorientation transition temperature. (b)–(f) Thermomagnetic curves for different samples under an applied magnetic field of 50 Oe under ZFC and FC conditions. Panels (b)–(f) correspond to samples P, Bp, Fp, Bv and Fv, respectively.
The curves for sample P show three transition temperatures. The two higher transition temperatures (230 and 97 K) are considered to be the paramagnetic-to-ferrimagnetic transition temperature $T_{\rm C}$ (the minima in the $\partial M/\partial T$ curves) and the magnetic freezing temperature $T_{\rm f}$ (the maxima in the $\partial M/\partial T$ curves), respectively. The ferrimagnetic region is between the Curie temperature and the freezing temperature. The splitting between the ZFC and FC curves for sample P is ascribed to the pinning of domain wall.[28–30] The irreversibility of the $M$–$T$ curve below $T_{\rm f}$ is due to the magnetic freezing effect, which is a characteristic of the spin-glass state. The transition from the ferrimagnetic state to the spin-glass state is called the re-entrant spin-glass-like transition.[27,31,32]
Table 1. Magnetic transition temperatures of different samples.
$T_{\rm c}$ (K) $T_{\rm f}$ (K) $T_{\rm rs}$ (K)
P 230 97 35
Bp 233 104 33
Bv 232 112 31
Fp 258 29
Fv 256 146 28
The appearance of the re-entrant spin-glass-like transition may be caused by frustration (i.e., no spin configuration can satisfy all the magnetic couplings simultaneously and minimize the energy) and randomness within the spin system.[28] The frustration of the spin systems originates from the geometric relation of the placements of the antiferromagnetic-coupled magnetic atoms. In the Ni$_{2}$In-type structure, Mn atoms in the octahedron (2$a$ sites) and triangle bipyramid (2$d$ sites) interact directly. Meanwhile, along the $c$ axis, Mn atoms in 2$a$ sites are arranged as linear chains, thus direct coupling occurs between spins. According to the curve of interaction energy versus Mn–Mn distance, the effective exchange integral between nearest-neighboring Mn atoms is negative (antiferromagnetic interaction). The nearest-neighboring 2$a$ and 2$d$ sites form a triangle so that the magnetic moments of antiferromagnetic coupling cannot be antiparallel with respect to any nearest-neighbor magnetic moment, which causes frustration. The randomness comes from the disordered arrangement of the atoms and holes within the Mn 2$d$ sublattice. The spin-reorientation transition appears at the lowest transition temperature (about 35 K). The magnetic transitions in the Bp, Bv, Fp and Fv samples are similar to those in sample P, but the transition temperatures differ. Table 1 lists the transition temperatures of all the samples. As can be seen from Table 1, Fp does not have a freezing temperature, which shows that no re-entrant spin-glass-like transition occurs because there is no frustration in the [100] direction. Meanwhile, the freezing temperatures $T_{\rm f}$ in the Bp, Bv, and Fv samples (104, 112 and 146 K, respectively) are significantly greater than that in sample P (97 K). Samples Bp and Bv have almost the same Curie temperature (233 and 232 K, respectively) as Fp and Fv (258 and 256 K, respectively), although sample F has a Curie temperature higher than sample P (230 K). In addition, the magnetic moments in sample F mostly focus on the Fv direction, as determined by comparing the results of Fp and Fv at 20 K (5.52 emu/g for Fp and 39.72 emu/g for Fv). Fv has a larger magnetic susceptibility, indicating that this direction may be the direction in which the net magnetic moment is arranged, which means that it is easy to magnetize in the direction of Fv. This conclusion is also confirmed in Fig. 3, which shows that Fv thoroughly saturates at 5000 Oe, whereas Fp saturates at 10000 Oe. Figure 3 shows the $M$–$H$ loops for the samples at different temperatures with an applied magnetic field of up to 8 T. The magnetization of all the oriented samples is well saturated in a field of 1 T, whereas sample P approaches saturation. However, the saturation magnetization differs significantly for the samples with different orientations. The saturation magnetization of Fp is the largest and reaches 72.6 emu/g. Sample Fv is the easiest to saturate (the saturation field is 5000 Oe), and sample Bv is the hardest to saturate (the saturation field is 1 T), which indicates anisotropy. Furthermore, almost no magnetic hysteresis appears except for Bv at 20 K, which indicates that Mn$_{2-\delta}$Sn undergoes a second-order magnetic transition.
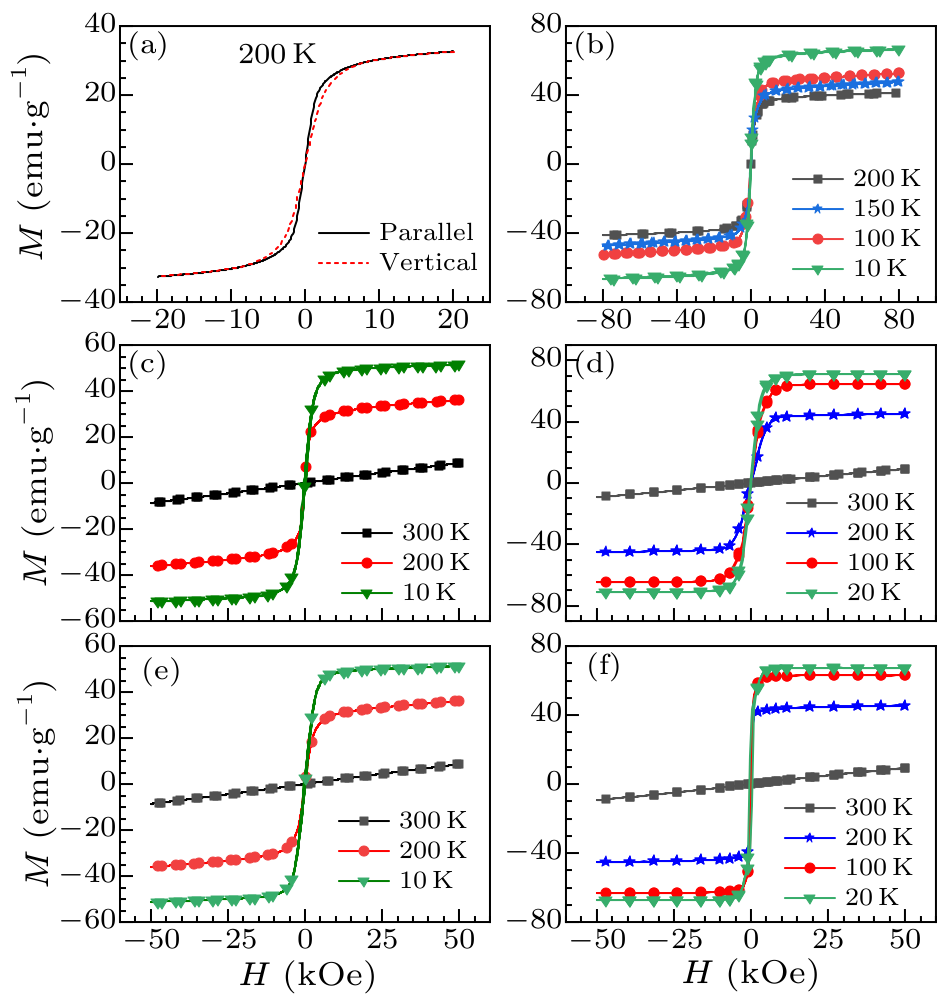
cpl-36-9-097502-fig3.png
Fig. 3. (a) The $M$–$H$ loops of Bp and Bv at 200 K with an applied magnetic field up to 2 T (Bv is harder to saturate than Bp). (b)–(f) The $M$–$H$ loops of different samples at different temperatures. Panels (b)–(f) correspond to samples P, Bp, Fp, Bv and Fv, respectively.
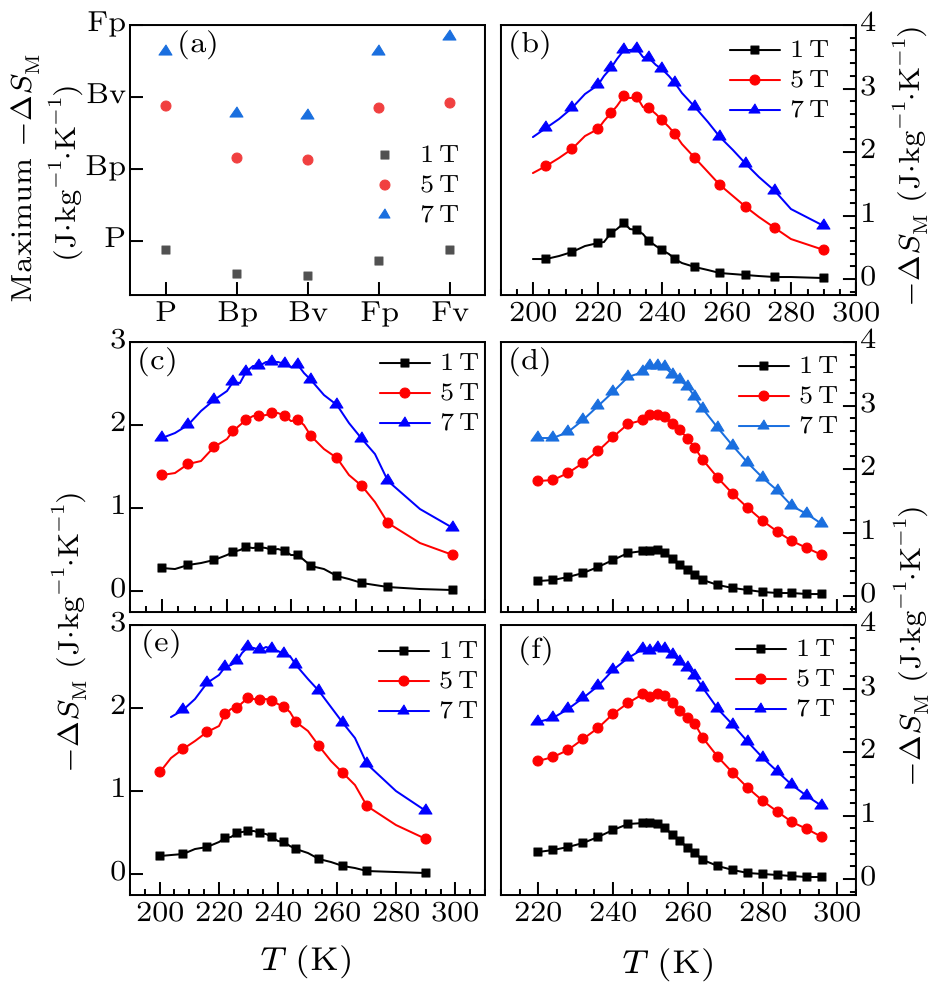
cpl-36-9-097502-fig4.png
Fig. 4. (a) Maximum $-\Delta S_{\rm M}$ for different samples with different applied magnetic fields. (b)–(f) Temperature dependence of magnetic entropy changes for different samples. Panels (b)–(f) correspond to samples P, Bp, Fp, Bv and Fv, respectively.
We measured the $M$–$H$ curves of the samples at different temperatures and calculated $-\Delta S_{\rm M}(T$) using the Maxwell relations (see Fig. 4). The maximum $-\Delta S_{\rm M}$ and the relative cooling power (RCP)[33,34] of different samples are listed in Table 2. RCP is calculated from the product of the maximum $|-\Delta S_{\rm M}|$, and the full width at half maximum of the peak in entropy changes versus temperature. The maximum $-\Delta S_{\rm M}$ and RCP for F are greater than those for B because of magnetocrystalline anisotropy. The sample Fv has the greatest maximum of $-\Delta S_{\rm M}$ and RCP, specifically, the greatest maximum of $-\Delta S_{\rm M}$ is 2.91 J$\cdot$kg$^{-1}$K$^{-1}$ (about one third of Gd) and 3.64 J$\cdot$kg$^{-1}$K$^{-1}$ at 5 and 7 T, and the corresponding RCPs are 212 and 302 J/kg, respectively. Accordingly, Fv has a considerable RCP and a wide working temperature (more than 80 K). However, the samples prepared by the same method show no significant difference in the maximum $-\Delta S_{\rm M}$ for a magnetic field applied in two mutually perpendicular directions, which indicates a small anisotropy. However, the RCP of sample Fv (212 J/kg at 5 T, and 302 J/kg at 7 T) exceeds that of sample Fp (174 J/kg at 5 T, and 286 J/kg at 7 T) because of the wider temperature span for sample Fv. In addition, the width of the peak in entropy change depends on the applied magnetic field, as the magnetic field $\Delta H$ increases, the width broadens. The properties make Mn$_{2-\delta}$Sn a promising material for a large potential application in the magnetic refrigeration over a wide range of temperatures.
Table 2. Maximum $-\Delta S_{\rm M}$ and RCPs for different samples.
Maximum $-\Delta S_{\rm M}$ (J$\cdot$kg$^{-1}\cdot$K$^{-1}$) RCP (J$\cdot$kg$^{-1}$)
$\Delta H=1$ T $\Delta H=5$ T $\Delta H=7$ T $\Delta H=$5 T $\Delta H=7$ T
P 0.88 2.88 3.62 201 296
Bp 0.54 2.15 2.76 185 251
Bv 0.52 2.12 2.74 182 260
Fp 0.72 2.85 3.62 174 286
Fv 0.88 2.91 3.64 212 302
In summary, we have prepared single-phase polycrystalline and oriented samples of Mn$_{2-\delta}$Sn alloys to study their magnetic properties. Almost all the samples undergo a re-entrant spin-glass-like transition and spin reorientation at low temperatures. The anisotropy of different oriented samples leads to different transition temperatures, saturation magnetizations, and maximum $-\Delta S_{\rm M}$. Sample Fv (applied magnetic field perpendicular to the [100] direction) is the easiest to magnetize and sample Bv (applied magnetic field perpendicular to the [101] direction) is the hardest to magnetize. The maximum magnetic entropy change also differs among different samples, and sample Fv has the largest value (maximum $-\Delta S_{\rm M}=2.91$ and 3.64 J$\cdot$kg$^{-1}$K$^{-1}$ with an applied magnetic field of 5 and 7 T, respectively). It also has the largest value of RCP (212 and 302 J/kg at 5 and 7 T, respectively). As the applied magnetic field $\Delta H$ increases, the maximum $-\Delta S_{\rm M}$ increases, which broadens the temperature range for refrigeration. References New Class of Materials: Half-Metallic FerromagnetsSpintronics: Fundamentals and applicationsSpintronics: A Challenge for Materials Science and Solid-State ChemistryHigh Spin Polarization of Ferrimagnetic Half-Heusler Compounds FeCrZ and MnYZ (Y=Mn, Cr; Z=IIIb, IVb, Vb Elements)Complete Spin Polarization for a Carbon Nanotube with an Adsorbed Atomic Transition-Metal ChainComplete spin polarization of electrons in semiconductor layers and quantum dotsA full spectrum of spintronic properties demonstrated by a C1 b -type Heusler compound Mn 2 Sn subjected to strain engineeringHalf-metallicity and magnetic properties of half-Heusler type Mn2Sn: Ab initio predictionsHeusler alloysFormation and coupling of magnetic moments in Heusler alloysStructural variants and the modified Slater-Pauling curve for transition-metal-based half-Heusler alloysIncreasing Curie temperature in tetragonal Mn 2 RhSn Heusler compound through substitution of Rh by Co and Mn by RhNew Mn 2 -based Heusler CompoundsMagnetism of hexagonal Mn 1.5 X 0.5 Sn (X = Cr, Mn, Fe, Co) nanomaterialsSimple rules for the understanding of Heusler compoundsDesign Scheme of New Tetragonal Heusler Compounds for Spin-Transfer Torque Applications and its Experimental RealizationMagnetic refrigeration: an eco-friendly technology for the refrigeration at room temperatureMagnetic refrigeration: recent developments and alternative configurationsOptimization of the physical properties of magnetocaloric materials for solid state magnetic refrigerationMagnetocaloric effect: From materials research to refrigeration devicesMagneto-optical properties of metallic ferromagnetic materialsMagnetic properties of the Mn1+xSb1−xSnx systemThe Fermi surface of rhodiumMagnetic Properties of Intermetallic Compounds in Manganese-Tin System: Mn 3.67 Sn, Mn 1.77 Sn, and MnSn 2The evolution of the magnetic phases of Sb-doped Mn 5 Sn 3 compoundsApparent spin‐glass nature of an anisotropic ferromagnetReentrant Spin Glass Behavior in Cr-Doped Perovskite ManganiteA Spin-Glass-Like State in the Ni2In-Type Mn7(Sn1–xGex)4 below the Ferrimagnetic StateLong-Time Decay of Thermoremanent Magnetization through Stepwise Changes of the Reentrant Spin-Glass-Like State in the Ni2In-Type Mn7Sn4Wide temperature span of entropy change in first-order metamagnetic MnCo 1− x Fe x Si
[1] Groot R A D, Mueller F M, Engen P G V and Buschow K H J 1983 Phys. Rev. Lett. 50 2024
[2] Zutic I, Fabian J and Sarma S D 2004 Rev. Mod. Phys. 76 323
[3] Felser C, Fecher G and Balke B 2007 Angew. Chen. Int. Ed. 46 668
[4] Fujii S, Ishida S and Asano S 2010 J. Phys. Soc. Jpn. 79 124702
[5] Yang C K, Zhao J J and Lu J P 2004 Nano Lett. 4 561
[6] Osipov V V, Petukhov A G and Smelyanskiy V N 2005 Appl. Phys. Lett. 87 202112
[7] Wang X T, Cheng Z X, Wang J L et al 2016 J. Mater. Chem. C 36 8535
[8] Luo H Z, Liu G D, Meng F B et al 2011 Physica B 406 4245
[9] Webster P J 1969 Contemp. Phys. 10 559
[10] Kubler J, Williams A R and Sommers C B 1983 Phys. Rev. B 28 1745
[11] Shaughnessy M, Fong C Y, Yang L H et al 2013 J. Appl. Phys. 113 043709
[12] Alijani V, Meshcheriakova O, Winterlik J et al 2013 J. Appl. Phys. 113 063904
[13] Kreiner G, Kalache A, Hausdorf S et al 2014 Z. Anorg. Allg. Chem. 640 738
[14] Fuglsby R, Kharel P, Zhang W et al 2015 J. Appl. Phys. 117 17D115
[15] Graf T, Felser C and Parkin S S P 2011 Prog. Solid State Chem. 39 1
[16] Winterlik J, Chadov S, Gupta A et al 2012 Adv. Mater. 24 6283
[17] Aprea C, Greco A, Maiorino A et al 2015 J. Phys.: Conf. Ser. 655 01206
[18] Almanza M, Kedous-Lebouc A, Yonnet J P et al 2015 Eur. Phys. J-Appl. Phys. 71 10903
[19] Silva D J, Bordalo B D, Puga J et al 2016 Appl. Therm. Eng. 99 514
[20] Franco V, Blázquez J S, Ipus J J et al 2018 Prog. Mater. Sci. 93 112
[21] Buschow K H J, van Engen P G and Jongebreur R 1983 J. Magn. Magn. Mater. 38 1
[22] Vasilev E A and Gelyasin A E 1978 Phys. Status Solidi 47 K55
[23]Howotny H and Schubert K 1946 Z. Metallkd. 37 17
[24]Kaplienko A I, Leonov B N and Chekin V V 1969 Solid State Phys. 11 3030
[25] Satya M N S, Begum R J, Srinivasan B S et al 1965 Phys. Lett. 15 223
[26]Shiraishi H, Hori T, Ohkubo N et al 2010 Phys. Status Solidi 1 3660
[27] Yasukōchi K, Kanematsu K and Ohoyama T 1961 J. Phys. Soc. Jpn. 16 1123
[28] Xu J H, Xia Y H, Yang W Y et al 2013 J. Appl. Phys. 113 17E111
[29] Griffith G, Volkening F A and Claus H 1985 J. Appl. Phys. 57 3392
[30] Dho J, Kim W S and Hur N H 2002 Phys. Rev. Lett. 89 027202
[31] Hagiwara N, Matoba M, Fujii S et al 1993 Phys. Status Solidi B 176 K71
[32] Isogai Y, Kobayashi T, Yoshida T et al 1997 Phys. Status Solidi 203 213
[33]Gschneidner K A and Jr. Pecharsky V K 2000 Annu. Rev. Mater. Res. 30 387
[34] Xu J H, Yang W Y, Du Q H et al 2014 J. Phys. D 47 065003