⇦Chinese Physics Letters, 2017, Vol. 34, No. 2, Article code 020601 Realization of Closed-Loop Operation of Optical Lattice Clock Based on $^{171}$Yb * Hui Liu(刘慧)1,2, Xi Zhang(张曦)1,2, Kun-Liang Jiang(姜坤良)1,2, Jin-Qi Wang(王进起)1,2, Qiang Zhu(朱强)1, Zhuan-Xian Xiong(熊转贤)1**, Ling-Xiang He(贺凌翔)1, Bao-Long Lyu(吕宝龙)1** Affiliations 1Key Laboratory of Atomic Frequency Standards, Wuhan Institute of Physics and Mathematics, Chinese Academy of Sciences, wuhan 430071 2University of Chinese Academy of Sciences, Beijing 100049 Received 28 November 2016 *Supported by the National Natural Science Foundation of China under Grant Nos 61227805, 91536104, 11574352, 11274349 and 91636215, and the Strategic Priority Research Program of the Chinese Academy of Sciences under Grant No XDB21030700.
**Corresponding author. Email: zxxiong@wipm.ac.cn; baolong_lu@wipm.ac.cn Citation Text: Liu H, Zhang X, Jiang K L, Wang J Q and Zhu Q et al 2017 Chin. Phys. Lett. 34 020601 Abstract We report the realization of closed-loop operation of an optical lattice clock based on $^{171}$Yb atoms. We interrogate the $^{1}\!S_{0}\rightarrow^{3}\!\!P_{0}$ clock transition using single Rabi pulses of 578 nm laser light. The two $\pi$-transitions from $m_{F}=\pm1/2$ ground states are alternatively interrogated, and the clock laser frequency is locked to the center of the two resonances. The in-loop error signal stability of the clock reaches $3\times10^{-17}$ for an average time of 3500 s. We also perform interleaved operations of the clock with two independent servo loops, and the fractional frequency difference averages down to $2\times10^{-16}$ in 7200 s. DOI:10.1088/0256-307X/34/2/020601 PACS:06.30.Ft, 37.10.Jk, 32.30.-r, 32.70.Jz © 2017 Chinese Physics Society Article Text Atomic clocks based on optical frequency have reached unprecedented stability and systematic accuracy,[1-8] surpassing the cesium (Cs) primary frequency standard as the definition of a second of the international system of units (SI). Redefinition of the SI second using atomic optical clocks is thus anticipated. State-of-the-art atomic optical clocks provide us not only with a more precise time and frequency standard but also advance frontiers of fundamental science such as tighter limits on fundamental constant variation,[7,9,10] hunting for topological dark matter[11] and clock-based geodesy.[12] Compared with optical clocks based on single ions, lattice clocks based on neutral atoms have much lower quantum projection noises, and hence much shorter measurement times. A detailed review on both trapped-ion clocks and lattice clocks was provided in Ref. [2]. Particularly, lattice clocks based on three species of neutral atoms ($^{87}$Sr, $^{171}$Yb and $^{199}$Hg) are being developed in China, and closed-loop operations have been reported for the $^{87}$Sr clock in NIM and $^{171}$Yb clock in ECNU.[13,14] The ytterbium ($^{171}$Yb) lattice clock is one of the most precise optical clocks. In 2013, the $^{171}$Yb clock in NIST set a new record for frequency stability ($1.6\times10^{-18}$ in 25000 s).[5] The $^{171}$Yb atom has the simplest hyperfine structure (nuclear spin $I=1/2$), offering two-fold advantages:[15] the simplest and most efficient optical pumping to the desired $m_{F}$ ground states, and the absence of tensor light shifts. In addition, the black-body-radiation- (BBR-) induced Stark shift of $^{171}$Yb is only half that of $^{87}$Sr, and its dynamic correction part is also smaller than that of $^{87}$Sr. Even at room temperature, the BBR-contributed uncertainty of $^{171}$Yb can be reduced to a level of $1\times10^{-18}$ by employing a well designed and controlled BBR shield.[16] Moreover, taking into account the electric-dipole, magnetic-dipole, and electric-quadrupole, polarizabilities and hyperpolarizabilities, a theoretical work predicted that the lattice-induced systematic uncertainty of the $^{171}$Yb clock can reach the $10^{-19}$ range if the lattice light is tuned to the so-called operational magic frequency.[17] In this Letter, we report the realization of a lattice clock based on $^{171}$Yb. The frequency instability has been evaluated using the atomic transition as a reference. The interleaved measurement technique based on two independent servo-loops has also been realized and used to measure the frequency difference. The experimental details about the cooling and trapping of $^{171}$Yb atoms, as well as the Rabi interrogation, have been described in recent works.[18-20] After two-stage magneto-optical cooling, about $2\times 10^{6}$ $^{171}$Yb atoms with a temperature of $\sim20\,μ$K are trapped in the green MOT operated on the 556 nm ${^{1}}S_{0}\rightarrow{^{3}}P_{1}$ transition. The atoms are then loaded into a one-dimensional optical lattice with a $1/e^{2}$ radius of 35 μm and a trap depth of $\sim$70 μK. Typically 30000 $^{171}$Yb atoms are prepared in the lattice for subsequent clock interrogation. The schematic diagram of the entire clock system and the time sequence for a typical experimental clock cycle are shown in Fig. 1. The frequency of the lattice light is monitored through a super-precise wavelength meter (HighFinesse GmbH, WSU-10) with an accuracy of 10 MHz, and locked at the magic wavelength of 759.35 nm to cancel the ac-Stark shift of the lattice light. Before clock transition interrogation, spin polarization must be carried out using circular polarized 556 nm laser light in resonance with the ${^{1}}S_{0}\rightarrow{^{3}}P_{1}$ transition.[18] With a pumping power of 5 μW, more than 99% of the atoms can be pumped to the desired spin state (either $m_{F}=-1/2$ or $m_{F}=1/2$). In this process, the heating effect and atomic loss can be ignored due to the weakness of the pumping beam. The bias magnetic field required for spin polarization is set to 0.2 mT, which can be calibrated using the Zeeman splitting between two spin states. For Rabi interrogation, a $\pi$ pulse of 578 nm laser light with an ultra-narrow linewidth is applied to excite atoms into the $^{3}P_{0}$ state. Subsequently a normalized shelving detection is performed to measure the excitation fraction.
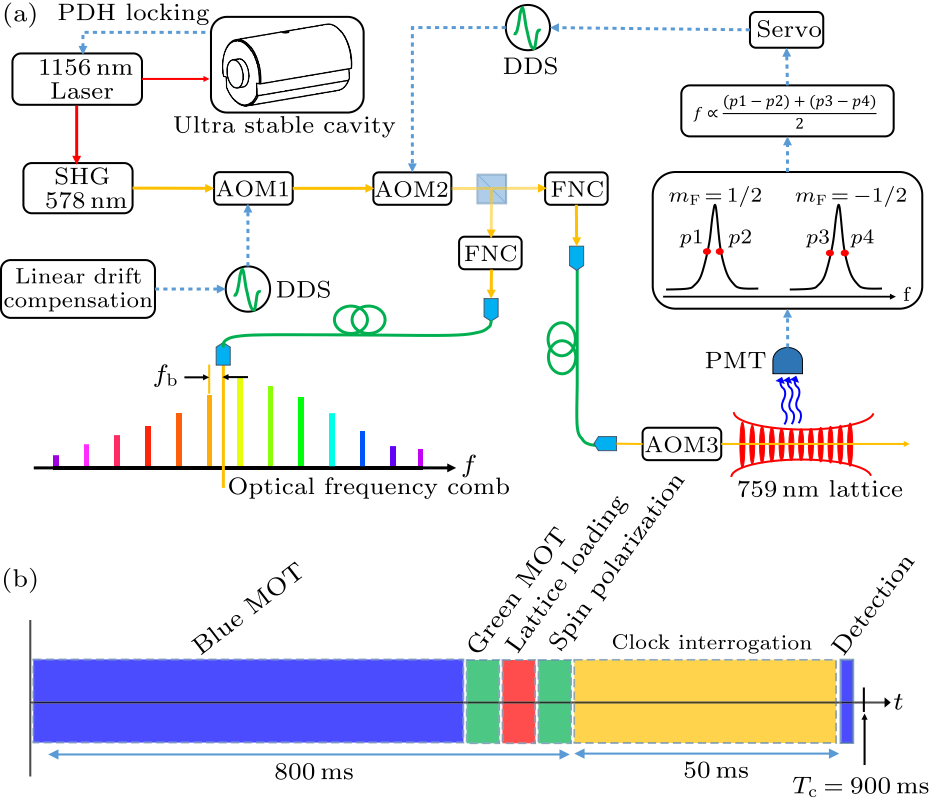
cpl-34-2-020601-fig1.png
Fig. 1. (Color online) (a) Schematic diagram for the $^{171}$Yb lattice clock. Clock laser at 578 nm is generated by frequency doubling of a 1156 nm semiconductor laser locked to an ultra-stable optical cavity, and then sent to the lattice system and an optical frequency comb for clock interrogation and frequency measurement. Fiber noise cancellation (FNC) systems are used to eliminate the phase noise introduced by fibers. The linear frequency drift of the clock laser is compensated through an acousto-optic modulator (AOM1). Experimental clock cycles alternately interrogate both $m_{F}$ spin states to cancel first-order Zeeman and vector Stark shifts. The frequency correction signal is obtained from the measured excitation ratios near the half maximum, and then used to steer the clock laser frequency through AOM2. AOM3 is used to modulate the clock laser to reach the spin states. (b) Timing sequence for a typical clock cycle of 0.9 s. The servo-loop generates a frequency correction signal every four clock cycles.
Theoretically, longer interrogation time is better for a narrower clock spectrum. However, the experimentally achievable linewidth in the clock spectroscopy is limited by various factors such as atomic interactions, atomic temperature, lifetime of the atoms in the lattice, as well as the misalignment between the interrogation beam and the lattice beam.[21] As shown in Fig. 2, for our system, a minimum linewidth of 5 Hz has been obtained with a 200-ms-long Rabi pulse, corresponding to a line quality factor of $Q=1\times10^{14}$. However, a robust locking to the clock transition requires that the linewidth must be much larger than the possible frequency excursion of the 578 nm clock laser in a timescale of a few clock cycles. As a compromise, a Rabi pulse duration of $T_{\rm i}=50$ ms was chosen for the closed-loop operation. In this case, the observed Rabi spectrum shows a linewidth of 18 Hz (see Fig. 2), which agrees well with the Fourier-limited linewidth ($0.89/T_{\rm i}=17.8$ Hz).
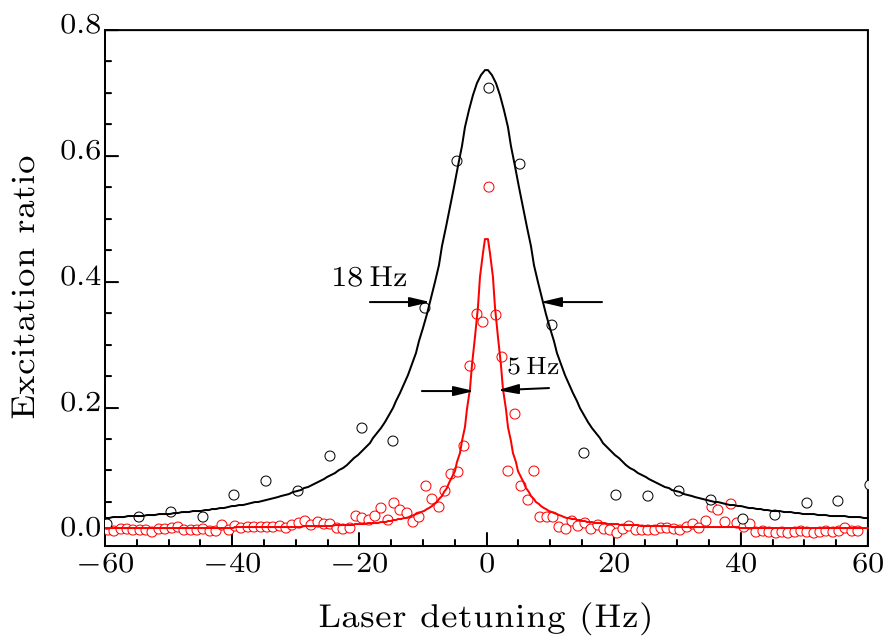
cpl-34-2-020601-fig2.png
Fig. 2. (Color online) Single-scan normalized excitation spectra of the $^{1}\!S_{0}\rightarrow^{3}\!\!P_{0}$ clock transition of $^{171}$Yb for Rabi interrogation. Black and red circles are the data for interrogation times of 50 ms and 200 ms, respectively. Solid curves are the Lorentzian fits to these data, giving nearly Fourier-limited linewidths of 18 Hz and 5 Hz, respectively.
An ultra-stable clock laser is crucial for both the clock interrogation and the closed-loop operation. Our 578 nm clock laser light is derived from frequency doubling a 1156 nm semiconductor laser. To reduce the linewidth and frequency drift, this laser is locked to a horizontally mounted ultra-stable reference cavity from stable laser systems. The cavity is made of an ultra-low-expansion (ULE) glass spacer and two fused-silica mirrors, having a cavity length of 10 cm and a finesse of $\sim4\times10^{5}$. It is placed in a vacuum system, and also temperature controlled to suppress the frequency fluctuations due to the environmental temperature change. According to the expressions in Refs. [22,23], the fractional frequency instability limit of the clock laser from the thermal noise of the cavity is calculated to be $4.2\times10^{-16}$. Since we have neither a second clock laser nor a second ULE cavity with comparable frequency stability levels, we are unable to measure the linewidth of the clock laser. On the other hand, the zero expansion temperature $T_{\rm C}$ of the cavity was not provided by the vendor. We had to measure it using the clock spectrum as a frequency reference. For each given cavity temperature, the deviation of the clock laser frequency from the atomic transition is measured. As shown in Fig. 3(a), $T_{\rm C}$ is determined to be 31.7(3)$^{\circ}\!$C. We set the cavity temperature to 31.7$^{\circ}\!$C, and did not find noticeable frequency drift in relation to the fluctuations of room temperature. However, cavity-aging-induced frequency drift remains. Figure 3(b) displays this kind of frequency drift during a time of 12 h. A linear drift rate of 60 mHz/s is inferred, which is at the same level as that of another group.[24] We also found that this drift rate is not constant due to unknown reasons, and it varies within a range of $\pm$20 mHz/s from day to day. Therefore, the linear drift compensation in the servo-loop need to be adjusted accordingly to improve the operation stability of the clock.
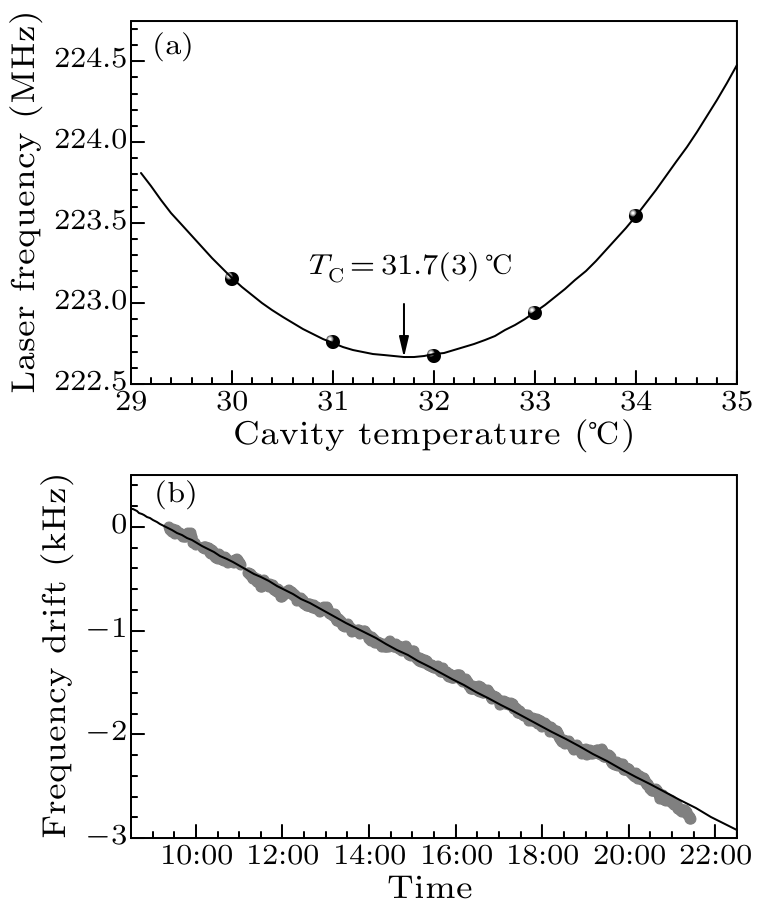
cpl-34-2-020601-fig3.png
Fig. 3. (a) The frequency of the 578 nm clock laser changes with the temperature of the ULE cavity. The solid line is a 2nd-order polynomial fit to the measured frequency values (solid circles), yielding a zero-expansion temperature of 31.7(3)$^{\circ\!}$C. (b) The measured frequency drift of the clock laser due to the cavity aging. A linear fit (black solid line) gives a drift rate of 60 mHz/s.
We then performed the closed-loop operation of the clock. In successive clock cycles, the two $m_{F}$ spin states are interrogated alternately to cancel the first-order Zeeman and vector Stark shifts. The error signal is calculated according to the differences of the measured excitation fractions at half maximum points of each Rabi spectrum (see Fig. 1). The corresponding frequency correction signal is then sent to AOM2 to lock the 578 nm laser to the clock transition. Our clock can operate continuously for more than 10 h, supporting an averaging time of 5000 s. To check the frequency instability of our clock, we first measured its frequency with an optical frequency comb referenced to a hydrogen maser (Vremya-CH, CH1-75 A). The Allan deviation of the beat note in 5000 s was found to be $3.2\times10^{-13}/\sqrt{\tau}$, in good agreement with the instability of the hydrogen maser. It indicates that the instability of our clock is much lower than the hydrogen maser. Frequency comparisons between two independent clocks would give a rigorous evaluation for the frequency instability. Without a second clock system, we have to evaluate the instability level using the clock transition as a reference, i.e., calculating the Allan deviation of the error signal (frequency correction signal).
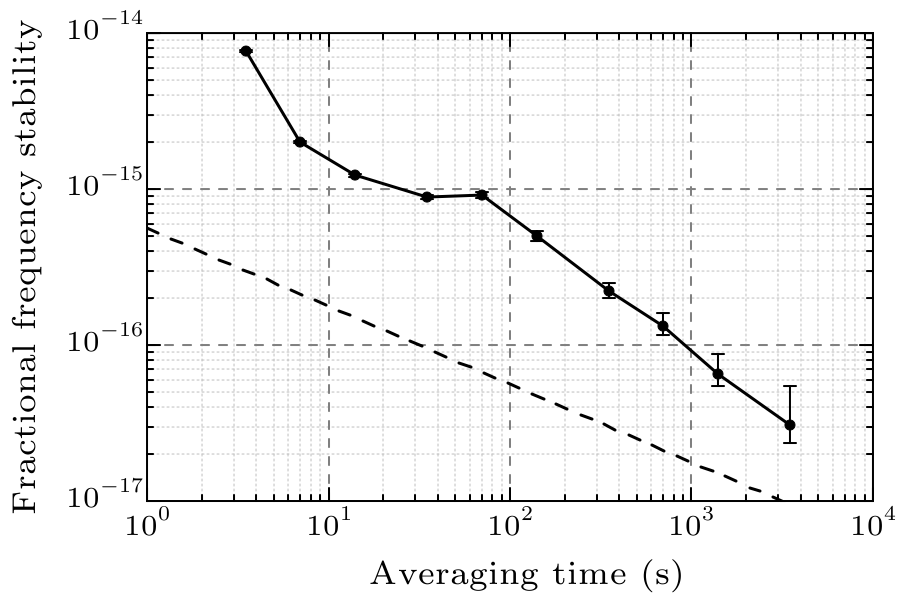
cpl-34-2-020601-fig4.png
Fig. 4. Instability evaluation of the $^{171}$Yb clock using atomic transition. Solid circles give the in-loop stability (from frequency correction signals) when the clock laser is locked to the atomic transition. The dashed line represents the calculated Dick-effect-limited instability of $5.6\times10^{-16}/\sqrt{\tau}$.
Figure 4 presents a typical in-loop fractional frequency instability for averaging times up to 3500 s. The Allan deviation does not drop smoothly in the range of 3.6–100 s. It is possibly due to the remaining frequency drift of clock laser which should exist if the linear frequency drift of the cavity is not ideally compensated. Therefore, at early times of the closed-loop operation, the frequency deviation from clock transition is relatively large. Beyond 70 s, the instability drops down quickly, and reaches $3\times10^{-17}$ at the averaging time of 3500 s. Note that this in-loop fractional frequency instability actually represents the lower limit to the expected clock instability,[22] rather than the clock instability itself. The Dick-effect limit under current experimental parameters is calculated to be $5.6\times10^{-16}/\sqrt{\tau}$ assuming that the instability of the clock laser is close to the thermal noise limit of our ULE cavity, and it is also plotted in Fig. 4. As we know that many physical effects can cause systematic frequency shift to an optical clock, an interleaved measurement technique is often employed to measure the systematic frequency shift, where a particular parameter of a clock is toggled between two settings in the interleaved clock cycles.[5,13] The frequency variation due to the parameter modulations can be obtained from frequency correction signals. The schematic diagram for the interleaved measurement of our clock is shown in Fig. 5. Two independent interrogation and feedback loops have been built to operate alternately with time. The frequency corrections $f_{1,2}$ are then fed back to their respective AOMs through two independent DDS systems to keep in-loop operations. In this interleaved measurement state, the time of the servo cycle is doubled, which will degrade the frequency stability of each servo-loop. Moreover, it means a more stringent requirement for the stability of the clock laser.
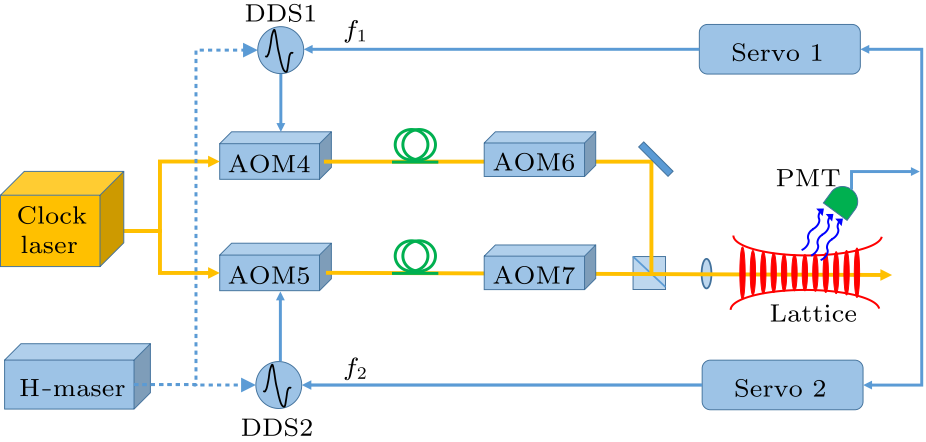
cpl-34-2-020601-fig5.png
Fig. 5. (Color online) The diagram for interleaved operation of the $^{171}$Yb lattice clock between two independent servo-loops which share the same clock laser. AOM4 and AOM5 are used for fiber noise cancelation and frequency servo control. The other two AOMs (AOM6 and AOM7) are used for frequency modulations of the interrogation beams, and also for the generation of interrogation pulses.
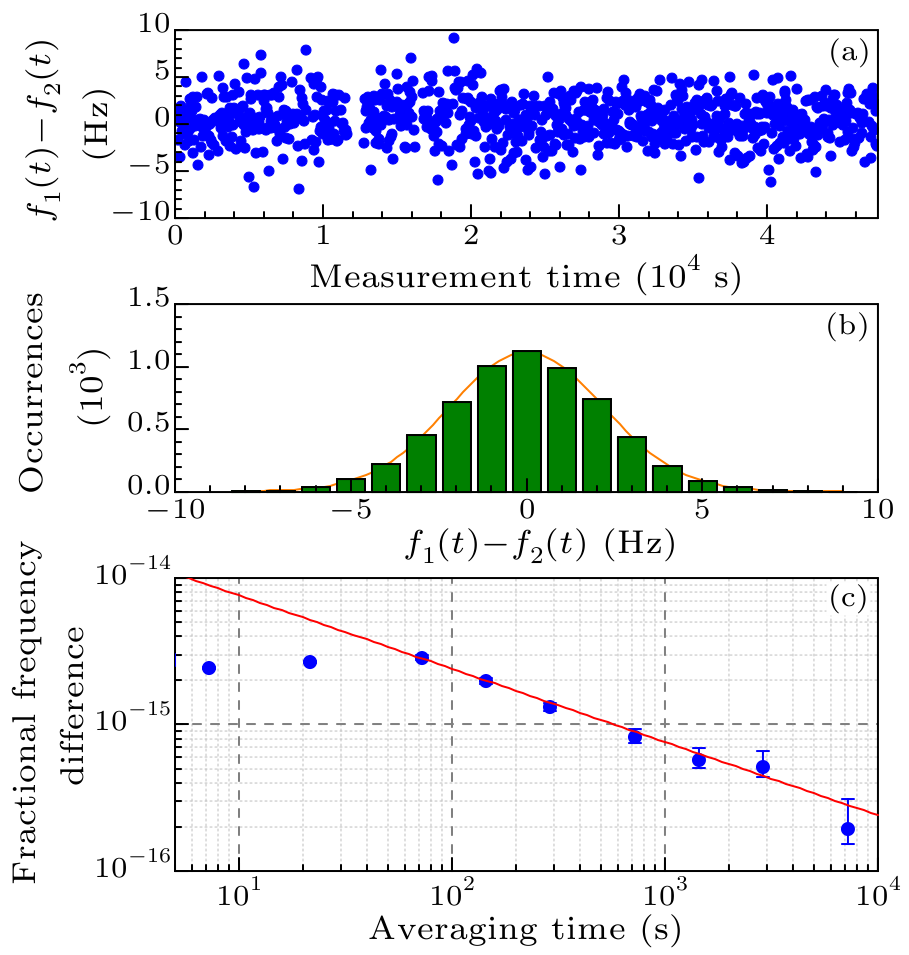
cpl-34-2-020601-fig6.png
Fig. 6. (Color online) The stability evaluation using the interleaved measurement method as illustrated in Fig. 5. The operation parameters of the clock are the same for the two interleaved servo-loops. (a) Frequency difference of the two correction frequencies, $f_{1}-f_{2}$, for a 48000 s time interval. (b) Histogram of all data and a Gaussian fit ($\chi^{2}_{r}=0.9994$). (c) Fractional frequency difference $f_{1}-f_{2}$. Red solid line represents a white-frequency-noise asymptote of $2.4\times10^{-14}/\sqrt{\tau}$.
To check the achievable precision in the measurement of frequency difference $f_{1}-f_{2}$, we allow the two servo-loops to operate at the same experimental parameters. The frequency corrections $f_{1,2}$ have been recorded for a time of 48000 s, and the data of $f_{1}-f_{2}$ is displayed in Fig. 6(a). A statistical histogram of the data is shown in Fig. 6(b), and the good match to the Gaussian fitting curve justifies the reliability of the data. Fractional stability of $f_{1}-f_{2}$ is shown in Fig. 6(c). The fractional stability at 10 s is less than $3\times10^{-15}$, which is dominated by the short-term stability of the clock laser. The instability starts to drop at $\sim$70 s, roughly ten times the feedback period. Fitting the data to a white-frequency-noise asymptote yields an instability of $2.4\times10^{-14}/\sqrt{\tau}$. A fractional stability of $2\times10^{-16}$ is achieved for an averaging time of 7200 s, representing the precision level for our interleaved measurement. In summary, we have constructed an optical lattice clock based on $^{171}$Yb and realize the closed-loop operation. A Rabi spectrum with a minimum width of 5 Hz has been obtained. The in-loop fractional instability (from error signal) of the clock reaches $3\times10^{-17}$ for an averaging time of 3500 s. Interleaved measurement based on two independent servo-loops have reached a precision of $2\times10^{-16}$. In the future, we will implement the evaluation of systematic uncertainty and the measurement of the absolute frequency of $^{171}$Yb clock transition. We acknowledge Ma L. S. for helpful discussion. References Systematic evaluation of an atomic clock at 2 × 10−18 total uncertaintyOptical atomic clocksSingle-Ion Atomic Clock with 3 × 10 − 18 Systematic UncertaintyAn optical lattice clock with accuracy and stability at the 10−18 levelAn Atomic Clock with 10-18 InstabilityFrequency Comparison of Two High-Accuracy Al + Optical ClocksFrequency Ratio of Two Optical Clock Transitions in Yb + 171 and Constraints on the Time Variation of Fundamental ConstantsFrequency Comparison of Two Ca + 40 Optical Clocks with an Uncertainty at the 10 − 17 LevelNew Limits on Coupling of Fundamental Constants to Gravity Using Sr 87 Optical Lattice ClocksImproved Limit on a Temporal Variation of m p / m e from Comparisons of Yb + and Cs Atomic ClocksHunting for topological dark matter with atomic clocksOptical Clocks and RelativityFirst Evaluation and Frequency Measurement of the Strontium Optical Lattice Clock at NIMSpin- 1 / 2 Optical Lattice ClockAtomic Clock with 1 × 10 − 18 Room-Temperature Blackbody Stark UncertaintyStrategies for reducing the light shift in atomic clocksHertz-Level Clock Spectroscopy of 171 Yb Atoms in a One-Dimensional Optical LatticeCreation of 174 Yb Bose—Einstein Condensates in a Crossed FORTObservation of Photoassociation Spectra of Ultracold 174 Yb Atoms at 1 S 0 — 3 P 1 Inter-Combination LineRabi spectroscopy and excitation inhomogeneity in a one-dimensional optical lattice clockMaking optical atomic clocks more stable with 10−16-level laser stabilizationContribution of thermal noise to frequency stability of rigid optical cavity via Hertz-linewidth lasersSubhertz linewidth diode lasers by stabilization to vibrationally and thermally compensated ultralow-expansion glass Fabry-Pérot cavities
[1] Nicholson T L et al 2015 Nat. Commun. 6 6896
[2] Ludlow A D et al 2015 Rev. Mod. Phys. 87 637
[3] Huntemann N et al 2016 Phys. Rev. Lett. 116 063001
[4] Bloom B J et al 2014 Nature 506 71
[5] Hinkley N et al 2013 Science 341 1215
[6] Chou C W et al 2010 Phys. Rev. Lett. 104 070802
[7] Godun R M et al 2014 Phys. Rev. Lett. 113 210801
[8] Huang Y et al 2016 Phys. Rev. Lett. 116 013001
[9] Blatt S et al 2008 Phys. Rev. Lett. 100 140801
[10] Huntemann N et al 2014 Phys. Rev. Lett. 113 210802
[11] Derevianko A and Pospelov M 2014 Nat. Phys. 10 933
[12] Chou C W et al 2010 Science 329 1630
[13] Lin Y G et al 2015 Chin. Phys. Lett. 32 090601
[14]Zhou M et al 2013 Asia-Pacific Radio Science Conference (Taipei 3–7 September 2013)
[15] Lemke N D et al 2009 Phys. Rev. Lett. 103 063001
[16] K Beloy et al 2014 Phys. Rev. Lett. 113 260801
[17] Katori H et al 2015 Phys. Rev. A 91 052503
[18] Zhang M J et al 2016 Chin. Phys. Lett. 33 070601
[19] Zhang M J et al 2014 Chin. Phys. Lett. 31 086701
[20] Long Y et al 2013 Chin. Phys. Lett. 30 073402
[21] Blatt S et al 2009 Phys. Rev. A 80 052703
[22] Jiang Y Y et al 2011 Nat. Photon. 5 158
[23] Notcutt M et al 2006 Phys. Rev. A 73 031804
[24] Alnis J et al 2008 Phys. Rev. A 77 053809