| CONDENSED MATTER: ELECTRONIC STRUCTURE, ELECTRICAL, MAGNETIC, AND OPTICAL PROPERTIES |
 |
|

|
|
|
Effective Bi-Layer Model Hamiltonian and Density-Matrix Renormalization Group Study for the High-$T_{\rm c}$ Superconductivity in La$_{3}$Ni$_{2}$O$_{7}$ under High Pressure |
| Yang Shen1, Mingpu Qin1,2*, and Guang-Ming Zhang3,4* |
1Key Laboratory of Artificial Structures and Quantum Control, School of Physics and Astronomy, Shanghai Jiao Tong University, Shanghai 200240, China
2Hefei National Laboratory, Hefei 230088, China
3State Key Laboratory of Low-Dimensional Quantum Physics and Department of Physics, Tsinghua University, Beijing 100084, China
4Frontier Science Center for Quantum Information, Beijing 100084, China
|
|
| Cite this article: |
|
Yang Shen, Mingpu Qin, and Guang-Ming Zhang 2023 Chin. Phys. Lett. 40 127401 |
|
|
|
|
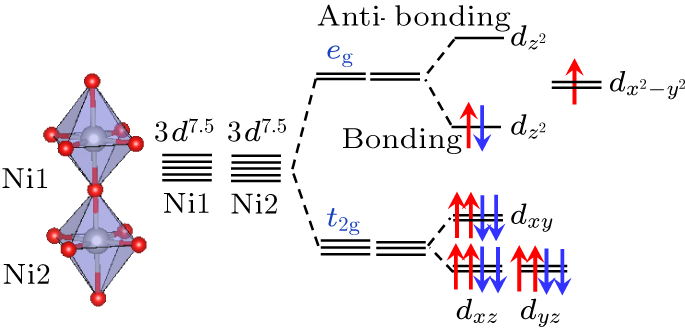
Abstract High-$T_{\rm c}$ superconductivity with possible $T_{\rm c}\approx 80$ K has been reported in the single crystal of ${\rm La}_{3}{\rm Ni}_{2}{\rm O}_{7}$ under high pressure. Based on the electronic structure given by the density functional theory calculations, we propose an effective bi-layer model Hamiltonian including both $3d_{z^{2}}$ and $3d_{x^{2}-y^{2}}$ orbital electrons of the nickel cations. The main feature of the model is that the $3d_{z^{2}}$ electrons form inter-layer $\sigma$-bonding and anti-bonding bands via the apical oxygen anions between the two layers, while the $3d_{x^{2}-y^{2}}$ electrons hybridize with the $3d_{z^{2}}$ electrons within each NiO$_2$ plane. The chemical potential difference of these two orbital electrons ensures that the $3d_{z^{2}}$ orbitals are close to half-filling and the $3d_{x^{2}-y^{2}}$ orbitals are near quarter-filling. The strong on-site Hubbard repulsion of the $3d_{z^{2}}$ orbital electrons gives rise to an effective inter-layer antiferromagnetic spin super-exchange $J$. Applying pressure can self dope holes on the $3d_{z^{2}}$ orbitals with the same amount of electrons doped on the $3d_{x^{2}-y^{2}}$ orbitals. By performing numerical density-matrix renormalization group calculations on a minimum setup and focusing on the limit of large $J$ and small doping of $3d_{z^{2}}$ orbitals, we find the superconducting instability on both the $3d_{z^{2}}$ and $3d_{x^{2}-y^{2}}$ orbitals by calculating the equal-time spin singlet pair–pair correlation function. Our numerical results may provide useful insights in the high-$T_{\rm c}$ superconductivity in single crystal La$_3$Ni$_2$O$_7$ under high pressure.
|
|
Received: 02 November 2023
Express Letter
Published: 21 November 2023
|
|
| PACS: |
74.70.-b
|
(Superconducting materials other than cuprates)
|
| |
74.90.+n
|
(Other topics in superconductivity)
|
|
|
|
|
|
| [1] | Li D F, Lee K, Wang B Y, Osada M, Crossley S, Lee H R, Cui Y, Hikita Y, and Hwang H Y 2019 Nature 572 624 |
| [2] | Nomura Y and Arita R 2022 Rep. Prog. Phys. 85 052501 |
| [3] | Li D F, Wang B Y, Lee K, Harvey S P, Osada M, Goodge B H, Kourkoutis L F, and Hwang H Y 2020 Phys. Rev. Lett. 125 027001 |
| [4] | Zeng S W, Tang C S, Yin X M et al. 2020 Phys. Rev. Lett. 125 147003 |
| [5] | Osada M, Wang B Y, Lee K, Li D, and Hwang H Y 2020 Phys. Rev. Mater. 4 121801 |
| [6] | Osada M, Wang B Y, Goodge B H, Harvey S P, Lee K, Li D, Kourkoutis L F, and Hwang H Y 2021 Adv. Mater. 33 2104083 |
| [7] | Zeng S W, Li C J, Chow L E, Cao Y, Zhang Z T, Tang C S, Yin X M, Lim Z S, Hu J X, Yang P et al. 2022 Sci. Adv. 8 eabl9927 |
| [8] | Anisimov V I, Bukhvalov D, and Rice T M 1999 Phys. Rev. B 59 7901 |
| [9] | Lee K W and Pickett W E 2004 Phys. Rev. B 70 165109 |
| [10] | Jiang M, Berciu M, and Sawatzky G A 2020 Phys. Rev. Lett. 124 207004 |
| [11] | Ikeda A, Krockenberger Y, Irie H, Naito M, and Yamamoto H 2016 Appl. Phys. Express 9 061101 |
| [12] | Zhang G M, Yang Y F, and Zhang F C 2020 Phys. Rev. B 101 020501 |
| [13] | Wang Z, Zhang G M, Yang Y F, and Zhang F C 2020 Phys. Rev. B 102 220501 |
| [14] | Wang N N, Yang M W, Yang Z, Chen K Y, Zhang H, Zhang Q H, Zhu Z H, Uwatoko Y, Gu L, Dong X L et al. 2022 Nat. Commun. 13 4367 |
| [15] | Sun H, Huo M, Hu X, Li J, Liu Z, Han Y, Tang L, Mao Z, Yang P, Wang B, Cheng J, Yao D X, Zhang G M, and Wang M 2023 Nature 621 493 |
| [16] | Pardo V and Pickett W E 2011 Phys. Rev. B 83 245128 |
| [17] | Gao M, Lu Z Y, and Xiang T 2015 Phys. Rev. B 91 045132 |
| [18] | Gao M, Lu Z Y, and Xiang T 2015 Physics 44 421 (in Chinese) |
| [19] | Dagotto E, Riera J, and Scalapino D 1992 Phys. Rev. B 45 5744 |
| [20] | Bulut N, Scalapino D J, and Scalettar R T 1992 Phys. Rev. B 45 5577 |
| [21] | Kuroki K, Kimura T, and Arita R 2002 Phys. Rev. B 66 184508 |
| [22] | Maier T A and Scalapino D J 2011 Phys. Rev. B 84 180513 |
| [23] | Mishra V, Scalapino D J, and Maier T A 2016 Sci. Rep. 6 32078 |
| [24] | Nakata M, Ogura D, Usui H, and Kuroki K 2017 Phys. Rev. B 95 214509 |
| [25] | Maier T A, Mishra V, Balduzzi G, and Scalapino D J 2019 Phys. Rev. B 99 140504 |
| [26] | Karakuzu S, Johnston S, and Maier T A 2021 Phys. Rev. B 104 245109 |
| [27] | Kato D and Kuroki K 2020 Phys. Rev. Res. 2 023156 |
| [28] | White S R 1992 Phys. Rev. Lett. 69 2863 |
| [29] | White S R 1993 Phys. Rev. B 48 10345 |
| [30] | de'Medici L, Hassan S R, Capone M, and Dai X 2009 Phys. Rev. Lett. 102 126401 |
| [31] | White S R and Chernyshev A L 2007 Phys. Rev. Lett. 99 127004 |
| [32] | Luo Z H, Hu X W, Wang M, Wú W, and Yao D X 2023 Phys. Rev. Lett. 131 126001 |
| [33] | Yang Q G, Wang D, and Wang Q H 2023 Phys. Rev. B 108 L140505 |
| [34] | Zhang Y, Lin L F, Moreo A, and Dagotto E 2023 arXiv:2306.03231 [cond-mat.supr-con] |
| [35] | Lechermann F, Gondolf J, Botzel S, and Eremin I M 2023 arXiv:2306.05121 [cond-mat.str-el] |
| [36] | Sakakibara H, Kitamine N, Ochi M, and Kuroki K 2023 arXiv:2306.06039 [cond-mat.supr-con] |
| [37] | Gu Y, Le C, Yang Z, Wu X, and Hu J 2023 arXiv:2306.07275 [cond-mat.supr-con] |
| [38] | Fishman M, White S R, and Stoudenmire E M 2022 SciPost Physics Codebases 4 |
|
|
Viewed |
|
|
|
Full text
|
|
|
|
|
Abstract
|
|
|
|
|