⇦Chinese Physics Letters, 2022, Vol. 39, No. 4, Article code 046401Express Letter High Mixing Entropy Enhanced Energy States in Metallic Glasses Juntao Huo (霍军涛)1, Kangyuan Li (李康源)2, Bowen Zang (臧博闻)1, Meng Gao (高萌)1, Li-Min Wang (王利民)3, Baoan Sun (孙保安)4, Maozhi Li (李茂枝)2*, Lijian Song (宋丽建)1*, Jun-Qiang Wang (王军强)1*, and Wei-Hua Wang (汪卫华)4 Affiliations 1CAS Key Laboratory of Magnetic Materials and Devices, and Zhejiang Province Key Laboratory of Magnetic Materials and Application Technology, Ningbo Institute of Materials Technology & Engineering, Chinese Academy of Sciences, Ningbo 315201, China 2Department of Physics, Renmin University of China, Beijing 100872, China 3State Key Lab of Metastable Materials Science and Technology, and College of Materials Science and Engineering, Yanshan University, Qinhuangdao 066004, China 4Institute of Physics, Chinese Academy of Sciences, Beijing 100190, China Received 23 February 2022; accepted 7 March 2022; published online 10 March 2022 *Corresponding authors. Email: jqwang@nimte.ac.cn; songlj@nimte.ac.cn; maozhili@ruc.edu.cn Citation Text: Huo J T, Li K Y, Zang B W et al. 2022 Chin. Phys. Lett. 39 046401    Abstract Owing to the nonequilibrium nature, the energy state of metallic glasses (MGs) can vary a lot and has a critical influence on the physical properties. Exploring new methods to modulate the energy state of glasses and studying its relationship with properties have attracted great interests. Herein, we systematically investigate the energy state, mixing entropy and physical properties of Zr–Ti–Cu–Ni–Be multicomponent high entropy MGs by experiments and simulations. We find that the energy state increases along with the increase of mixing entropy. The yield strength and thermal stability of MGs are also enhanced by high mixing entropy. These results may open a new door on regulation of energy states and thus physical properties of MGs.
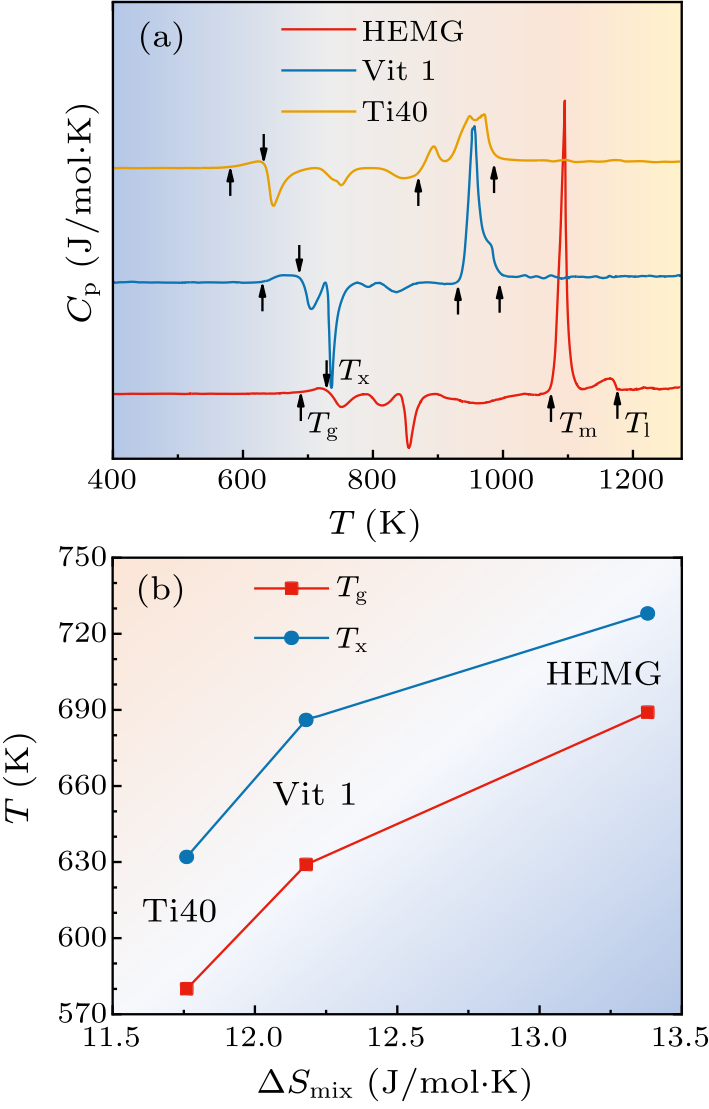
cpl-39-4-046401-fig1.png
cpl-39-4-046401-fig2.png
cpl-39-4-046401-fig3.png
cpl-39-4-046401-fig4.png
 DOI:10.1088/0256-307X/39/4/046401 © 2022 Chinese Physics Society Article Text Metallic glasses (MGs) have gained widespread attention due to their superior physical properties, such as high specific strength, high fracture toughness, good soft magnetic properties, and high corrosion resistance, compared to conventional crystalline materials.[1–5] MGs are nonequilibrium materials whose energy states can be widely changed and may have critical influence on physical properties.[6–27] Thus, modulating the energy state can design metallic glasses with advanced properties. The energy state of metallic glasses can be tailored by preparation process (e.g., cooling rate, pressure), relaxation, and rejuvenation, etc.[7–9] A faster cooling from melt usually yields a glass with higher energy, e.g., higher enthalpy and larger volume, which is usually accompanied with larger plasticity.[10,11] By applying pressurized quenching to a Zr-based metallic glass, a high-energy glass phase comparable to typical high-energy glass produced by rapid cooling was obtained.[12] Moreover, it is well known that structural relaxation of metallic glasses proceeds during thermal annealing processes at a temperature below the glass transition temperature $T_{\rm g}$, which is a structural ordering process and densifies atomic packing and reconfigures the atomic structure to a low-energy state, since there is a lack of volume-generating mechanisms at high temperatures.[13,14] Relaxation usually hardens and embrittles MGs, but can improve the soft magnetic properties of as-cooled Fe-based MGs.[15,16] Very recently, rejuvenation of metallic glasses has been achieved through various approaches, e.g., elastostatic compression, shot-peening, ion irradiation, and thermal cycling.[17–23] The rejuvenation processes can bring MGs to higher-energy states and thereby improve their plasticity and soft magnetic properties.[24–27] These previous researches show that the energy states of MGs can be regulated from the structural perspective. It is notable that the decrease of the enthalpy (i.e., energy state) of MGs during structural relaxation also depends on their chemical compositions.[28] Therefore, changing composition should be an effective means to tailor the energy state of MGs. However, there is no research to investigate the effect of compositions on the energy-states of metallic glasses so far. How to compare the energy states of different componential MGs is a burning question. In this study, the relationship between energy states and mixing entropy in metallic glasses is systematically investigated through thermodynamic characterization and simulation. Results show that the energy state can be tailored by mixing entropy, that is, the higher the mixing entropy, the higher the energy state. Moreover, the MGs with higher energy states also possess larger strengths from the componential perspective. Experimental and Simulation Methods. Three Zr–Ti–Cu–Ni–Be quinary metallic glasses with nominal compositions of Zr$_{20}$Ti$_{20}$Cu$_{20}$Ni$_{20}$Be$_{20}$ (HEMG),[29] Ti$_{40}$Zr$_{25}$Cu$_{12}$Ni$_{3}$Be$_{20}$ (Ti40)[30] and Zr$_{41}$Ti$_{14}$Cu$_{12.5}$Ni$_{10}$Be$_{22.5}$ (Vit 1)[31] were fabricated by arc melting of high purity Zr, Ti, Cu, Ni and Be metals and then cast into cylindrical rods (2 mm in diameter) by copper mold casting. The thermal characterization of three metallic glasses was performed by conventional differential scanning calorimetry (DSC 404 C). To avoid the oxidation of the samples, a high purity Ar gas flow (100 ml/min) was performed during the measurements. The sample was heated from room temperature to $T_{\rm h}=1273$ K with a heating rate $R_{\rm h}$ of 20 K/min, and the phase transition temperatures were determined. Afterwards, the heat capacity of the samples can be calculated from the heat flow traces. The ab initio molecular dynamics (MD) simulation with a canonical NVT (constant atom number, volume, and temperature) ensemble was performed by the Vienna ab initio simulation package (VASP),[32] in which the atomic forces can be determined with the first-principle calculations without using any experimental input or empirical potentials. Therefore, reliable atomic structures for liquid and amorphous materials can be successfully obtained.[33] A projected augmented wave method[34] and generalized gradient approximation[35] were used to describe the electron-ion interactions. The temperature was controlled using the Nose–Hoover thermostat. There were 200 atoms with specific compositions arranged in a cubic box with periodic boundary conditions applied in three directions. The simulation was performed on the $\varGamma$ point only. Three compositions of Zr$_{20}$Ti$_{20}$Cu$_{20}$Ni$_{20}$Be$_{20}$, Zr$_{25}$Ti$_{40}$Cu$_{12}$Ni$_{3}$Be$_{20}$ and Zr$_{41}$Ti$_{14}$Cu$_{12.5}$Ni$_{10}$Be$_{22.5}$ were calculated. The ensembles were first melted and equilibrated at 2000 K for 15 ps with time step of 3 fs, and then instantaneously cooled down to 600 K, 500 K, 400 K, 300 K, 200 K, and 100 K, respectively. The ensembles were then equilibrated for 15 ps at each. The density was adjusted corresponding to the zero pressure at each temperature. Results and Discussion. Figure 1 demonstrates the DSC curves of the three as-cast samples. All the samples show a clear endothermic glass transition process followed by several exothermic peaks correlating with crystallization processes and endothermic peaks corresponding to the melting behavior. The glass transition temperature $T_{\rm g}$, initial crystallization temperature $T_{\rm x}$, melting temperature $T_{\rm m}$, and liquidus temperature $T_{\rm l}$ are marked with arrows. We find that the phase transition temperature of HEMG is higher than the Vit 1 and Ti40, reflecting the high thermal stability of HEMG. To evaluate the glass forming ability, the supercooled liquid region $\Delta T$ ($\Delta T=T_{\rm x}-T_{\rm g}$), the reduced glass transition temperature $T_{\rm rg}$ ($T_{\rm rg}=T_{\rm g}/T_{\rm l}$), and the $\gamma$ parameter $[\gamma =T_{\rm x}/(T_{\rm g}+T_{\rm l})]$ are calculated and listed in Table 1.
cpl-39-4-046401-fig1.png
Fig. 1. (a) DSC curves of as-cast Zr$_{20}$Ti$_{20}$Cu$_{20}$Ni$_{20}$Be$_{20}$ (HEMG), Zr$_{41}$Ti$_{14}$Cu$_{12.5}$Ni$_{10}$Be$_{22.5}$ (Vit 1) and Ti$_{40}$Zr$_{25}$Cu$_{12}$Ni$_{3}$Be$_{20}$ (Ti40) metallic glasses. (b) The dependences of glass transition temperature $T_{\rm g}$ and initial crystallization temperature $T_{\rm x}$ on the mixing entropy $\Delta S_{\rm mix}$.
Table 1. The glass transition temperature $T_{\rm g}$, initial crystallization temperature $T_{\rm x}$, melting temperature $T_{\rm m}$, liquidus temperature $T_{\rm l}$, the supercooled liquid region $\Delta T$, reduced glass transition temperature $T_{\rm rg}$, and $\gamma$ parameter for HEMG, Vit 1 and Ti40. Here, temperatures are in units of K.
$T_{\rm g}$ (K) $T_{\rm x}$ (K) $T_{\rm m}$ (K) $T_{\rm l}$ (K) $\Delta T$ $T_{\rm rg}$ $\gamma$
HEMG 689 728 1073 1176 39 0.586 0.390
Vit 1 629 686 930 995 57 0.632 0.422
Ti40 580 632 870 986 52 0.588 0.403
To quantify the high entropy effect, the mixing entropy of the three alloys can be calculated by $$ \Delta S_{\rm mix}=-R\sum\limits_{i=1}^n {c_{i}\ln c_{i}},~~ \tag {1} $$ where $R$ is the gas constant, $c_{i}$ is the molar fraction of the $i$th element, and $n$ is the total number of constituent elements. The $\Delta S_{\rm mix}$ of HEMG, Vit 1 and Ti40 are 13.38 J$\cdot$mol$^{-1}$$\cdot$K$^{-1}$, 12.18 J$\cdot$mol$^{-1}$$\cdot$K$^{-1}$, and 11.76 J$\cdot$mol$^{-1}$$\cdot$K$^{-1}$, respectively. Interestingly, the thermal stability increases with the increase of $\Delta S_{\rm mix}$, as shown in Fig. 1(b), which is analogous to that of the polymer materials.[36] Although the HEMG exhibits a poor glass forming ability than Vit 1 and Ti40, the performance in glassy state was retained due to the high thermal stability.
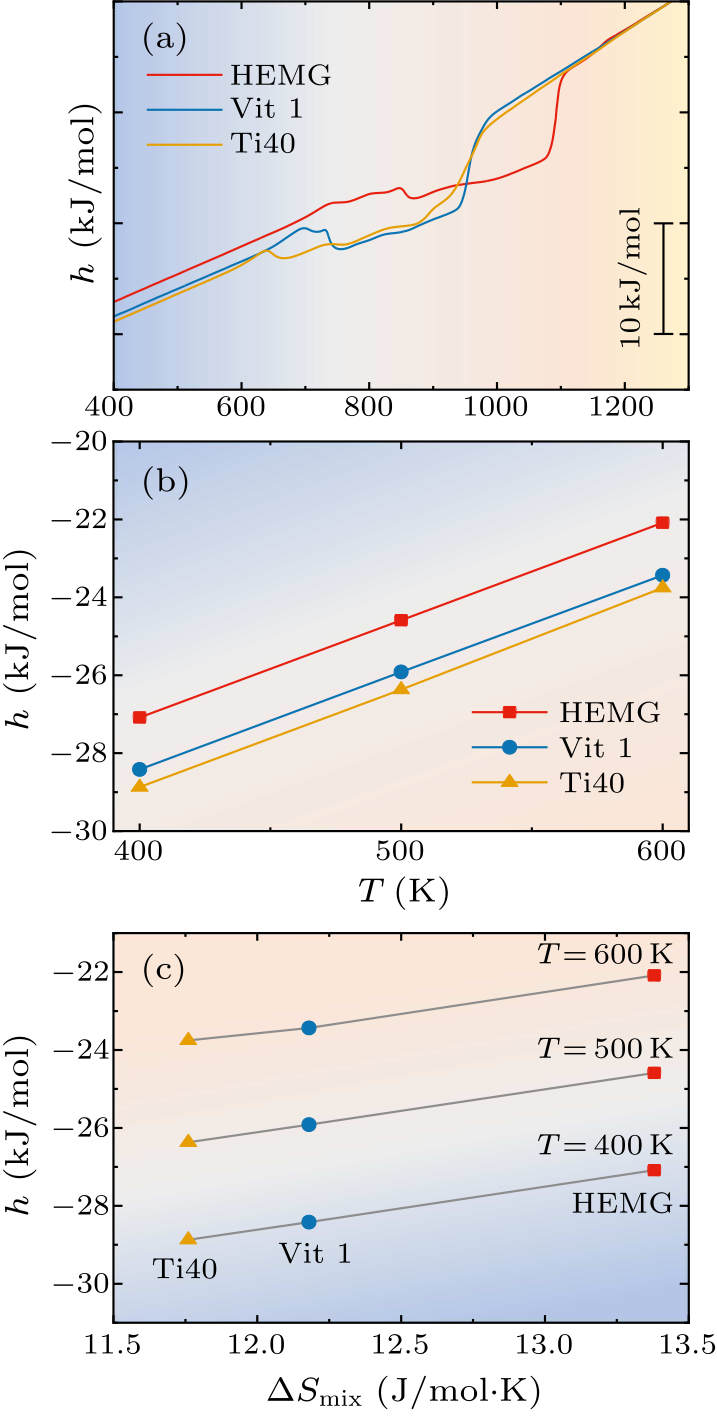
cpl-39-4-046401-fig2.png
Fig. 2. (a) The relative enthalpy of HEMG, Vit1 and Ti40 metallic glasses. (b) The relative enthalpy of the three samples at three representative temperatures $T=400,\, 500$ and 600 K. (c) The relationship between enthalpy changes and mixing entropy at 400, 500 and 600 K, respectively.
Thermodynamically, the heat capacity of a glass follows the empirical equations: $$ C_{\rm p}(T)=\frac{3R}{M}\Big[1-{\exp}\Big(-\frac{1.5T}{T_{\rm D}}\Big)\Big],~~ \tag {2} $$ where $T_{\rm D}$ is the Debye temperature and $M$ is close to 1.[37] Therefore, the specific heat capacity of the sample should be close to $3R$ in glassy state. On the other hand, the difference of heat capacity between glassy state and supercooled liquid is around $1.5R$.[38] Furthermore, the $C_{\rm p}$ can be obtained by the heat flow signals:[39] $$ C_{\rm p}(T)=\frac{\dot{Q}(T)}{MR_{\rm h}},~~ \tag {3} $$ where $\dot{Q}$ is the heat flow (W/g), $M$ is the molar mass, and $R_{\rm h}$ is the heating rate. The enthalpies of the three samples are calculated by $$ h(T)=\int_{_{\scriptstyle \rm RT}}^{T_{\rm h}} {C_{\rm p}(T)dT},~~ \tag {4} $$ where RT stands for the room temperature, $T_{\rm h}=1273$ K is the final temperature of the equilibrium liquid state. Here, we assume the enthalpy of the equilibrium liquid state at $T_{\rm h}=1273$ K is 0 kJ/mol. In Fig. 2(a), we can find that the energy state of HEMG in the glassy state is always higher than those of Vit 1 and Ti40, indicating that the HEMG can inheritance more energy from the equilibrium liquid. To provide a clear picture of the enthalpy change with temperature, the enthalpies at three representative temperatures $T = 400,\, 500$ and 600 K are shown in Fig. 2(b). For a given temperature $T = 400$ K, the enthalpies of HEMG, Vit 1 and Ti40 are $-27.09$ kJ/mol, $-28.41$ kJ/mol, and $-28.87$ kJ/mol, respectively. Especially, the energy states of the three samples increase with the increase of $\Delta S_{\rm mix}$, as shown in Fig. 2(c). This result reveals a strong link between the energy state and entropy. For the HEMG, the random atomic rearrangement of sample cooled from liquid tends to inherit more defects from the liquid. The low entropy samples should have a bad memory of the liquid state. Thus, the glasses with high entropy exhibit a good thermal stability and a high energy state, which are suitable for thermoplastic deformation.
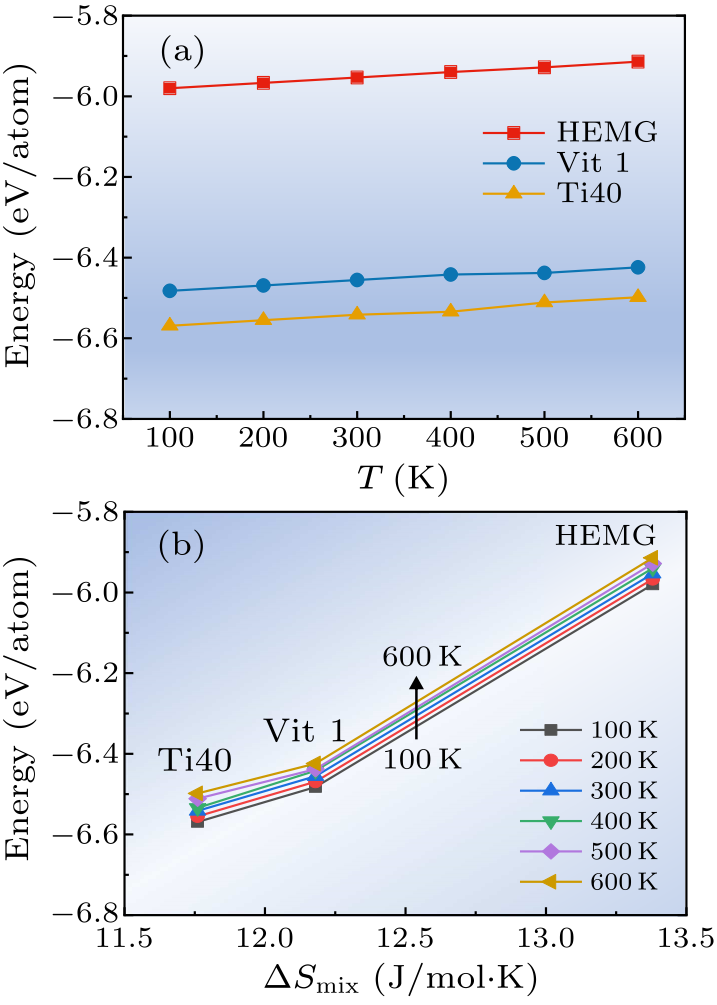
cpl-39-4-046401-fig3.png
Fig. 3. (a) The energy per atom for HEMG, Vit1 and Ti40 metallic glasses at 100, 200, 300, 400, 500, and 600 K, respectively. (b) The dependence of energy on mixing entropy $\Delta S_{\rm mix}$.
To further confirm the influence of mixing entropy on the energy state of MGs, ab initio MD simulation with a canonical NVT ensemble was performed by the VASP. Figure 3 shows the energy per atom for the three compositions at 100, 200, 300, 400, 500, and 600 K, respectively. There is a noticeable increase in the total energy with the increasing temperature, as shown in Fig. 3(a). Moreover, the energy level also increases linearly with the mixing entropy [see Fig. 3(b)]. As is expected, high entropy MG attains a higher energy level. We note that different concentrations of an element could change the energy level. For example, Zr concentration is significantly different in the three MGs, and the high entropy metallic glass contains less Zr content, which would cause its higher energy. However, this is not the case because the Zr$_{41}$Ti$_{14}$Cu$_{12.5}$Ni$_{10}$Be$_{22.5}$ MG contains more Zr, whereas its energy level is not the lowest. For other elements, the situation is similar. Therefore, the simulation results also demonstrate that the energy states can be enhanced by high mixing entropy in MGs.
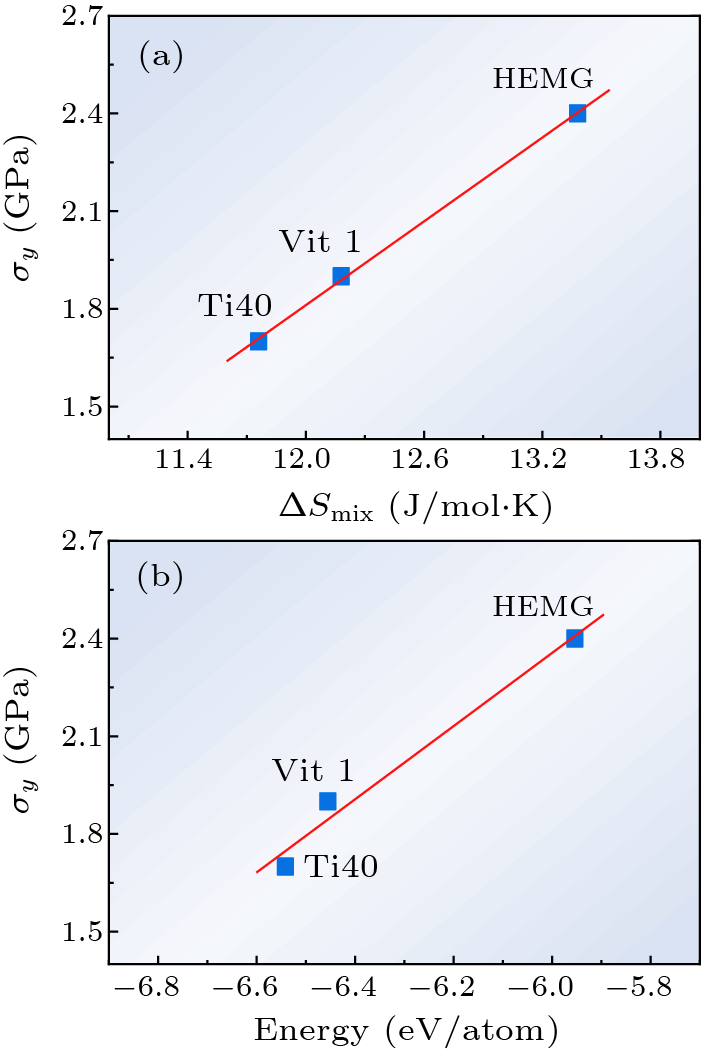
cpl-39-4-046401-fig4.png
Fig. 4. The dependences of yield strength $\sigma_{y}$ on the (a) mixing entropy $\Delta S_{\rm mix}$, and (b) energy at 300 K.
In general, the MGs with higher energy states possess larger strengths.[19,25] The yield strengths ($\sigma_{y}$) of HEMG, Vit 1 and Ti40 approximately are 2.4 GPa, 1.9 GPa, and 1.7 GPa, respectively.[29–31] Figure 4 shows the mixing entropy and energy state dependences of yield strength. It can be found that the yield strength shows a linearly relationship to both mixing entropy and energy state. The larger $\sigma_{y}$ of HEMG compared to those of Vit 1 and Ti40 indicates that the MGs with higher energy states possess larger yield strength from the point of view of chemical composition. From the above results, it can be concluded that the mechanical properties and even other physical properties of MGs can be adjusted by changing energy states via regulating mixing entropy. In summary, the influence of mixing entropy on the energy states in metallic glasses is systematically investigated. Both thermal experiments and MD simulations verify that the energy states of high-entropy MGs are higher than that of low entropy MGs. It is significant that the MGs with higher energy states also possess higher yield strengths and higher thermal stability. These results provide a new strategy to regulate the energy states and thus physical properties of metallic glasses from the componential perspective. Acknowledgments. We acknowledge financial supports from the National Key R&D Program of China (Grant Nos. 2018YFA0703602 and 2018YFA0703604), the National Natural Science Foundation of China (Grant Nos. 51922102 and 51827801), Youth Innovation Promotion Association CAS (Grant No. 2019296), and the Zhejiang Provincial Natural Science Foundation of China (Grant No. LR22E010004). References Bulk Metallic Glasses with Functional Physical PropertiesProcessing of Bulk Metallic GlassBulk metallic glassesThe elastic properties, elastic models and elastic perspectives of metallic glassesA New Cu-Based Metallic Glass Composite with Excellent Mechanical Properties*Dynamic Crossover in Metallic Glass Nanoparticles*Rejuvenation in Hot-Drawn Micrometer Metallic Glassy Wires*A free energy landscape perspective on the nature of collective diffusion in amorphous solidsThermomechanical processing of metallic glasses: extending the range of the glassy statePlasticity of a TiCu-based bulk metallic glass: Effect of cooling rateEffects of cooling rates on the mechanical properties of a Ti-based bulk metallic glassProperties of high-density, well-ordered, and high-energy metallic glass phase designed by pressurized quenchingDynamic relaxations and relaxation-property relationships in metallic glassesGlass Dynamics Deep in the Energy LandscapeStructural origin of magnetic softening in a Fe-based amorphous alloy upon annealingThe evolution of relaxation modes during isothermal annealing and its influence on properties of Fe-based metallic glassRejuvenation Behaviors in Metallic GlassesStructural evolution in deformation-induced rejuvenation in metallic glasses: A cavity perspectiveComposition dependence of mechanically-induced structural rejuvenation in Zr-Cu-Al-Ni metallic glassesRejuvenation by weakening the medium range order in Zr46Cu46Al8 metallic glass with pressure preloading: A molecular dynamics simulation studyVarious Rejuvenation Behaviors of Zr-Based Metallic Glass by Cryogenic Cycling Treatment with Different Casting TemperaturesThermal rejuvenation in metallic glassesPrediction of pressure-promoted thermal rejuvenation in metallic glassesPotential energy states and mechanical properties of thermally cycled binary glassesThe effect of cryogenic thermal cycling on aging, rejuvenation, and mechanical properties of metallic glassesImproved tensile plasticity of bulk metallic glasses by heightening microstructural heterogeneity and energy stateSerrated magnetic properties in metallic glass by thermal cycleRelationship between the enthalpies of structural relaxation, crystallization and melting in metallic glass-forming systemsStructure transformation and fractography in Zr20Ti20Cu20Ni20Be20 metallic glassDuctile titanium-based glassy alloy ingotsDeformation behavior of the Zr41.2Ti13.8Cu12.5Ni10Be22.5 bulk metallic glass over a wide range of strain-rates and temperaturesEfficient iterative schemes for ab initio total-energy calculations using a plane-wave basis setAtomic packing and short-to-medium-range order in metallic glassesProjector augmented-wave methodCorrelation hole of the spin-polarized electron gas, with exact small-wave-vector and high-density scalingEntropy of Mixing and the Glass Transition of Amorphous MixturesHeat capacity of oxide glasses at high temperature regionCorrelation between dynamic flow and thermodynamic glass transition in metallic glasses
[1] Wang W H 2009 Adv. Mater. 21 4524
[2] Schroers J 2010 Adv. Mater. 22 1566
[3] Wang W H, Dong C, and Shek C H 2004 Mater. Sci. Eng. R 44 45
[4] Wang W H 2012 Prog. Mater. Sci. 57 487
[5] Li D M, Chen L S, Yu P, Ding D, and Xia L 2020 Chin. Phys. Lett. 37 086401
[6] Zhang S, Wang W, and Guan P 2021 Chin. Phys. Lett. 38 016802
[7] Dong J, Feng Y H, Huan Y, Yi J, Wang W H, Bai H Y, and Sun B A 2020 Chin. Phys. Lett. 37 017103
[8] Wang Y J, Du J P, Shinzato S, Dai L H, and Ogata S 2018 Acta Mater. 157 165
[9] Sun Y, Concustell A, and Greer A L 2016 Nat. Rev. Mater. 1 16039
[10] Shen J, Huang Y J, and Sun J F 2007 J. Mater. Res. 22 3067
[11] Xiao Y, Wu Y, Liu Z, Wu H, and Lue Z 2010 Sci. Chin. Phys. Mech. & Astron. 53 394
[12] Miyazaki N, Lo Y C, Wakeda M, and Ogata S 2016 Appl. Phys. Lett. 109 091906
[13] Wang W H 2019 Prog. Mater. Sci. 106 100561
[14] Ediger M D, Gruebele M, Lubchenko V, and Wolynes P G 2021 J. Phys. Chem. B 125 9052
[15] Tong X, Zhang Y, Wang Y, Liang X, Zhang K, Zhang F, Cai Y, Ke H, Wang G, Shen J, Makino A, and Wang W 2022 J. Mater. Sci. & Technol. 96 233
[16] He N, Song L, Xu W, Huo J, Wang J Q, and Li R W 2019 J. Non-Cryst. Solids 509 95
[17] Pan J and Duan F 2021 Acta Metall. Sin. 57 439
[18] Jiang S, Huang Y, and Li M 2019 Chin. Phys. B 28 046103
[19] Qiang J and Tsuchiya K 2017 J. Alloys Compd. 712 250
[20] Feng S D, Chan K C, Zhao L, Pan S P, Qi L, Wang L M, and Liu R P 2018 Mater. & Des. 158 248
[21] Guo W, Yamada R, Saida J, Lu S, and Wu S 2018 Nanoscale Res. Lett. 13 398
[22] Saida J, Yamada R, Wakeda M, and Ogata S 2017 Sci. Technol. Adv. Mater. 18 152
[23] Miyazaki N, Wakeda M, Wang Y J, and Ogata S 2016 npj Comput. Mater. 2 16013
[24] Priezjev N V 2019 J. Mater. Res. 34 2664
[25] Priezjev N V 2019 J. Non-Cryst. Solids 503 131
[26] Ma Y B, Mei L, Cui X, and Zu F Q 2021 Kovove Mater.-Metallic Mater. 59 181
[27] Ri M C, Sohrabi S, Ding D W, Dong B S, Zhou S X, and Wang W H 2017 Chin. Phys. B 26 066101
[28] Afonin G V, Mitrofanov Y P, Kobelev N P, Pinto M W D S, Wilde G, and Khonik V A 2019 Scr. Mater. 166 6
[29] Wang J G, Yang H, Pan Y, Song Y J, Li W H, and He Y Z 2016 J. Non-Cryst. Solids 452 273
[30] Guo F Q, Wang H J, Poon S J, and Shiflet G J 2005 Appl. Phys. Lett. 86 091907
[31] Lu J, Ravichandran G, and Johnson W L 2003 Acta Mater. 51 3429
[32] Kresse G and Furthmuller J 1996 Phys. Rev. B 54 11169
[33] Sheng H W, Luo W K, Alamgir F M, Bai J M, and Ma E 2006 Nature 439 419
[34] Blöchl P E 1994 Phys. Rev. B 50 17953
[35] Wang Y and Perdew J P 1991 Phys. Rev. B 44 13298
[36] Pinal R 2008 Entropy 10 207
[37] Inaba S, Oda S, and Morinaga K 2003 J. Non-Cryst. Solids 325 258
[38] Ke H B, Wen P, Zhao D Q, and Wang W H 2010 Appl. Phys. Lett. 96 251902
[39]Höhne G, McNaughton J, Hemminger W, Flammersheim H J, and Flammersheim H J 2003 Differential Scanning Calorimetry 2nd edn (New York: Springer Science & Business Media) p 147