⇦Chinese Physics Letters, 2021, Vol. 38, No. 1, Article code 017102 Disorder and Itinerant Magnetism in Full Heusler Pd$_2$TiIn Guanhua Qin (秦冠华)1,2, Wei Ren (任伟)1*, David J. Singh2,3*, and Bing-Hua Lei (雷兵华)2* Affiliations 1Physics Department, Shanghai Key Laboratory of High Temperature Superconductors, State Key Laboratory of Advanced Special Steel, MGI and ICQMS, Shanghai University, Shanghai 200444, China 2Department of Physics and Astronomy, University of Missouri, Columbia, MO 65211, USA 3Department of Chemistry, University of Missouri, Columbia, MO 65211, USA Received 9 October 2020; accepted 23 November 2020; published online 6 January 2021 Supported by the National Natural Science Foundation of China (Grant Nos. 51861145315, 51672171, 12074241, and 51911530124), the Department of Energy, Basic Energy Sciences (Award DE-SC0019114) for work at the University of Missouri, the Shanghai Municipal Science and Technology Commission Program (Grant No. 19010500500), the China Scholarship Council (CSC), the Independent Research Project of State Key Laboratory of Advanced Special Steel and Shanghai Key Laboratory of Advanced Ferrometallurgy at Shanghai University, and the State Key Laboratory of Solidification Processing in NWPU (Grant No. SKLSP201703).
*Corresponding authors. Email: renwei@shu.edu.cn; singhdj@missouri.edu; bl6cb@missouri.edu Citation Text: Qin G H, Ren W, Singh D J, and Lei B H 2021 Chin. Phys. Lett. 38 017102    Abstract We report electronic and magnetic properties of full Heusler Pd$_2$TiIn based on first principles calculations. This compound has been variously characterized as magnetic or non-magnetic. We use first principles calculations with accurate methods to reexamine this issue. We find that ideal ordered Heusler Pd$_2$TiIn remains non-magnetic, in accord with prior work. However, we do find that it is possible to explain the magnetism seen in experiments through disorder and in particular we find that site disorder can lead to moment formation in this compound. In addition, we find an alternative low energy cubic crystal structure, which will be of interest to explore experimentally. DOI:10.1088/0256-307X/38/1/017102 © 2021 Chinese Physics Society Article Text The $A_2BC$ Heusler compounds are a very large set of cubic materials, with exceptionally diverse and often tunable properties.[1–4] One area of particular interest has been magnetism and spin polarized transport, since a number of the compounds show both high ferromagnetic Curie temperatures and high spin polarization.[3–15] This includes half-metals such as Co$_2$MnSi (note in the following we use the notion $A_2BC$, for the Heusler structure compounds rather than the IUPAC notation listing elements in order of increasing electronegativity). In addition, there is interest in Heusler materials with spin-orbit coupling, as this can rotate spins and provide magnetocrystalline anisotropy. Furthermore, the high symmetry of the cubic Heusler structure can lead to band crossings with Dirac dispersions. One material that has been studied in this regard is Pd$_2$TiIn, which is a metal that occurs in the cubic full Heusler structure and is predicted to have Dirac dispersions, related to band crossings near the Fermi level along the face centered cubic (FCC) $\varGamma$–$X$ line in the absence of magnetism.[16] However, the origins of the magnetic behavior of this compound are unclear. Finally, it is noteworthy that Heusler compounds near magnetism have been of strong interest for thermoelectric effects and related energy conversion applications.[17,18] The Pd$_2$Ti$Z$ ($Z$ = Al, In, Sn) compounds have attracted interest and discussion over the past twenty years. Pd$_2$TiAl is reported to be ferromagnetic, but with a small moment relative to its Curie temperature and therefore this may instead be superparamagnetism. Furthermore, there is apparently sample dependence, while ferromagnetism with a very low moment was also reported in Pd$_2$TiSn.[19–24] Similar contradictory results are found for Pd$_2$TiIn. Measured susceptibility data show a broad maximum at $\sim $110 K, along with a very large moment from high temperature Curie–Weiss fitting of $\sim$4.9$\mu_{\rm B}$. This led to the suggestion that the compound may be an itinerant antiferromagnet.[7] However, subsequent neutron scattering studies on samples that did have the susceptibility peak around $\sim 110$ K nonetheless showed no antiferromagnetism. On the other hand, a first order structural transition was found at lower temperature.[25] The measurements did not exclude weak ferromagnetism, which was conjectured to exist. These results motivated first principles studies. Jaswal reported calculations using the linearized-muffin-tin-orbital (LMTO) method with the atomic sphere approximation (ASA), finding no ferromagnetism for either the cubic or the reported low temperature tetragonal structure,[26] while Jezierski and co-workers reported a similar result, also using the LMTO method with shape approximations.[21,24,27] The purpose of the present study is to elucidate the properties of cubic Pd$_2$TiIn in detail using modern all-electron methods with no shape approximations and specifically to address the properties of the compound in relation to experimental observations of magnetic behavior. We find, in agreement with prior studies, that fully ordered stoichiometric Pd$_2$TiIn is not ferromagnetic. This intermetallic material is characterized as an itinerant, large Fermi surface metal. We find additionally that the compound has low energy defects including both antisites and vacancies that can be present. We also find that site disorder involving the Ti atoms either directly or through induced changes in Ti bond lengths can lead to magnetic behavior. This offers a possible explanation for the various experimental observations. We note that this is in accord with defect studies of other materials where magnetism can result from high concentrations of suitable defects. This includes magnetism induced by doping,[28,29] as well as non-dopant point defects such as in Fe$_2$VAl.[30–32] We also find a possible low energy phase with a different cubic structure. It will be of interest to experimentally search for this phase. The results on the interplay between moment formation and defects suggest experimental investigation of the dependence of magnetic properties on synthesis conditions. Computational Methods. We did density functional theory (DFT) calculations using the linearized augmented planewave (LAPW) method[33] as implemented in the WIEN2k code.[34] This is an all-electron method that makes no shape approximations, such as the ASA, and uses a flexible basis set in all regions of space, specifically, planewaves in the interstitial, and products of numerical radial functions and spherical harmonics in atom centered spheres. Here we use the accurate standard linearized augmentation with local orbitals,[35] as opposed to the more computationally efficient augmented planewave plus local orbital method.[36] The present calculations included local orbitals for treatment of semicore states, specifically the 4$p$ states of Pd, the 3$s$ and 3$p$ states of Ti and the 4$d$ states of In. We used a convergence criterion of $R_{\min}K_{\max}=9.0$, where $R_{\min}$ is the smallest LAPW sphere radius, and $K_{\max}$ is the planewave sector cutoff. This is generally considered to be sufficient for highly converged calculations for transition element containing compounds. Nonetheless, we tested this by repeating fixed spin moment calculations with higher values of $R_{\min}K_{\max}$, finding no significant changes. We did calculations with different choices of LAPW sphere radii as an additional test. The sphere radii used for this ranged from 2.35 bohr to 2.5 bohr for Pd and Ti and were 2.45 and 2.5 bohr for In. The Brillouin zone sampling was carried out using uniform meshes, and tests were performed to verify convergence. For example, the fixed spin moment calculations were implemented with a $30 \times 30 \times 30$ mesh in the Brillouin zone, and similarly converged meshes were used for other calculations. Core states were treated relativistically, while valence states were treated at a minimum in a scalar relativistic approximation. Additionally, we did some calculations incorporating spin orbit coupling (SOC) for the valence states as well, as described below. Calculations were performed with two different functionals, specifically the local density approximation (LDA), similar to prior work, and the generalized gradient approximation (GGA) of Perdew, Burke and Ernzerhof (PBE).[37] The thermopower was calculated using the BoltzTraP code with the constant scattering time approximation.[38] Except as noted, calculations were implemented using the experimental lattice parameter $a=6.365$ Å, which was reported by Neumann and co-workers.[7] Results and Discussion—Structure and Magnetic Order. The cubic full Heusler $A_2BC$ compounds, of which Pd$_2$TiIn is one, occur in the centrosymmetric spacegroup $Fm\bar{3}m$, with $A$ on Wycoff site 8$c$ (0.25,0.25,0.25), $B$ and $C$ on sites 4$b$ (0.5,0.5,0.5) and 4$a$ (0,0,0), respectively. Thus the $B$ and $C$ atoms can be viewed as forming rock-salt lattice, while the $A$ atoms occupy interstitials in this lattice. Commonly, $A$ and $B$ are transition elements and $C$ is a main group element. While this is not universal, it is the case in Pd$_2$TiIn. The stability of the full-Heusler structure has been discussed using valence electron count, electronegativity, atomic size and covalency, and all of these can be important.[2–4,39,40] Heusler $A_2BC$ compounds generally have the element with the most valence electrons on the $A$ site. Additionally, covalency involving especially the main group element is important. Also, a large electronegativity difference between the $B$ and $C$ atoms is stabilizing since the $B$ and $C$ atoms form a rock-salt lattice, which can be stabilized by ionic interactions. In Pd$_2$TiIn, Pd has the largest number of valence electrons, which is favorable for the full Heusler structure, but also has a substantially higher electronegativity (2.20) than Ti (1.54) or In (1.78), which may suggest a relative instability of the ordered structure. This is similar to the case of Fe$_2$VAl, where there is significant disorder. It should also be noted that the ordered Heusler structure does not readily accommodate differences in atomic size, due to the fixed bond lengths determined by the lattice parameter. This frustration may be related to the very low thermal conductivities in full Heusler[41] and related half-Heusler compounds (compounds with half of the $A$ sites empty), which leads to good thermoelectric performance in many half Heusler compounds,[42–45] and may also lead to superconductivity associated with soft modes.[46] In any case, in the present compound, each Pd is coordinated by four Ti and four In atoms at a distance of $d=\sqrt{3}a/4$ (= 2.756 Å, with the experimental lattice parameter), while the Ti and In are both coordinated by eight Pd atoms at the same distance of $d=\sqrt{3}a/4$. Considering these coordinations, one notes that the metallic radius of In is larger than that of Ti by[47] $\sim $0.19 Å, which also suggests lower stability for the compound, especially considering that charge transfer from Ti, as may be expected from the electronegativities, would enhance this size difference. The above factors lead to an expectation that defect formation energies may be relatively low, as we find (see below). Our DFT calculations yield a lattice parameters of 6.31 Å, and 6.46 Å, for the LDA and PBE functionals, respectively. These are within the typical errors compared with experiment for these two functionals, and in particular the LDA lattice parameter is slightly smaller (by 0.9%) than experiment, while the PBE functional is slightly larger (by 1.5%). As mentioned, neutron scattering measurements found no ordered antiferromagnetism but did identify a transition to a tetragonal structure in samples with a susceptibility maximum, similar to that associated with possible magnetism. This tetragonal structure was refined to be an $I4/mmm$ structure, which is the same as the cubic full Heusler structure with a strain leading to a $c/a$ different from unity.[25] We did PBE calculations examining this over the lattice parameter range from the experimental lattice parameter to the larger PBE lattice parameter. We find that there is no such symmetry lowering strain predicted for the ordered compound, and instead the cubic compound is stable over the lattice parameter range studied.
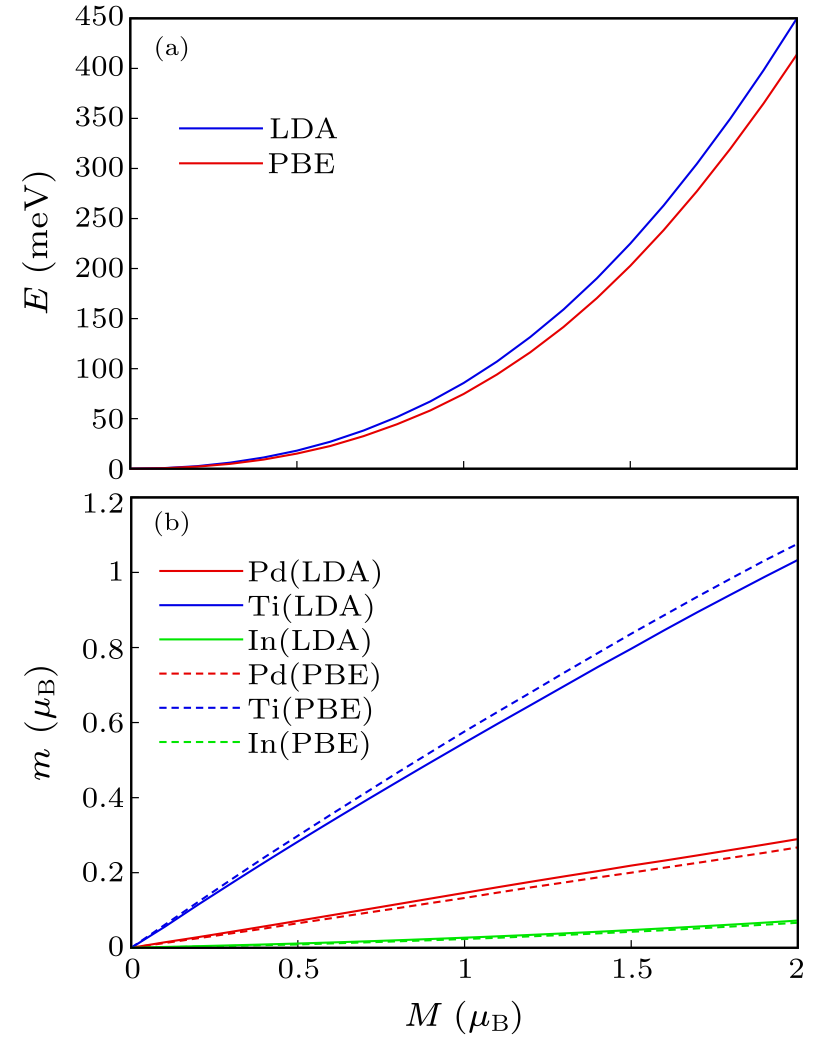
cpl-38-1-017102-fig1.png
Fig. 1. Fixed spin moment energy as a function of magnetization on a per formula unit basis, using the LDA and PBE functionals (a), and moment in single LAPW spheres in the fixed spin moment calculations (b). The fixed spin moment calculations were performed in a scalar relativistic approximation, with LAPW sphere radii of 2.5 bohr.
We now turn to the magnetism for the ordered compound. We did fixed spin moment calculations[48] in a scalar relativistic approximation at the experimental lattice parameter for both the LDA and PBE functional. The results are shown in Fig. 1. The smooth monotonic increase of energy with magnetization shows no ferromagnetic instability. As is typical,[49,50] the PBE functional is closer to ferromagnetism. This is shown by the lower energy cost relative to LDA for imposing a magnetization. We also did self-consistent calculations including SOC, but again find no ferromagnetic state. We additionally did calculations for the PBE functional at the larger predicted lattice parameter of the functional, but again find no ferromagnetic instability. It may also be noted that in some materials near magnetism, including some weak itinerant ferromagnets and materials near ferromagnetism, including Pd, quantum spin fluctuations may renormalize the properties.[51,52] These renormalizations can be strong, as has been discussed for the Sr$_3$Ru$_2$O$_7$, which is near a quantum critical point.[53] In general these spin-fluctuations tend to suppress magnetic ordering. If significant in Pd$_2$TiIn they would therefore move the material further from magnetism and would not change the conclusion that stoichiometric ordered Pd$_2$TiIn is not magnetic. It is in general possible to add terms to the Hamiltonian as in the LDA+$U$ method[54] in order to obtain magnetic behavior. While these are important in strongly correlated materials such as oxide Mott insulators, they are generally inappropriate in itinerant metals, and for example lead to strongly enhanced magnetism compared with experiment in materials such as Fe, Ni and Pd.[50,55,56] Considering that Pd$_2$TiIn is an intermetallic compound with strong hybridization and itinerant metallic character, we do not add such terms. Importantly, when a magnetization is imposed in Pd$_2$TiIn by the fixed spin moment method, it occurs almost entirely on the Ti, with only a small component involving Pd. This is as seen in the lower panel of Fig. 1. Electronic Structure. We note that there are two Pd atoms in the primitive unit cell. An antiferromagnetic arrangement of these would be consistent with the neutron scattering results. However, we checked for such a solution and did not find any stable magnetic state of this type. We also used supercell calculations searching for an antiferromagnetic solution. Specifically, we implemented calculations in the four formula conventional unit cell allowing the possibility of different arrangements of Ti moments. However, again we find no magnetic solutions. Thus we conclude that it is highly likely that ordered stoichiometric Pd$_2$TiIn is not magnetic in DFT calculations. Figure 2 shows that band structure and electronic density of states (DOS), $N(E)$, as obtained at the experimental lattice parameter with the PBE functional including SOC. The band structure around the Fermi level is similar to that presented by Mondal and co-workers,[16] including the presence of a band crossing along $\varGamma$–$X$, although the distance from the Fermi energy is slightly different. It is noteworthy that there are flat bands near the Fermi level along several directions in the zone, for example, along $\varGamma$–$L$ and $\varGamma$–$X$. These lead to a peak in $N(E)$ near the Fermi level. This peak has mixed character but is predominantly derived from Ti $d$ states. Turning to the large scale features of the DOS, the $d$ bands start at $\sim$$ -5.75$ eV relative to the Fermi level, $E_{\rm F}$. The main Pd $d$ bands provide a broad peak in the DOS from the bottom of the $d$ bands to $\sim $$-2$ eV, and a smaller peak around $-1$ eV, with a tail extending to the Fermi level. Thus the Pd $d$ bands are nominally full in this compound. This is in contrast to Pd metal, which has a high Pd $d$ contribution to the DOS at and around $E_{\rm F}$. This is as shown in the lower panel of Fig. 2 and leads to nearness to ferromagnetism in bulk Pd. The difference is due to narrower Pd $d$ band manifold in Pd$_2$TiIn, as seen in the comparison, although it should be noted that there is some Pd $d$ character at and above the Fermi level, due to hybridization with In states.
cpl-38-1-017102-fig2.png
Fig. 2. Band structure (a) and electronic density of states (DOS) and projections of $d$ character onto Pd and Ti, on a per formula unit basis (b). The Fermi level $E_{\rm F}$ is at 0 eV. These were calculated with the PBE functional including spin orbit. The projections were onto LAPW spheres of radius 2.5 bohr. (c) The DOS for bulk Pd metal. Note the position of the $d$-bands relative to $E_{\rm F}$.
In any case, the implication is that Pd moments are unlikely in this compound. This is in accord with the results of the fixed spin moment calculations, as discussed above. The Ti $d$ bands are primarily in the energy range from $-1$ eV to 3 eV, and dominate the DOS near $E_{\rm F}$. Thus magnetism, if any, is expected to be associated with the partially filled $d$ orbitals of Ti. Angle integrated photoemission experiments for Pd$_2$TiIn were reported by Brown and co-workers.[57] These measurements were carried out at different photon energies in order to separate the Pd and Ti contributions to the occupied electronic structure. They show a valence band width of slightly less than 6 eV, in very close accord with the calculations. They also show a prominent Pd derived peak between 2 eV and 4 eV binding energy, which is very similar to the Pd component of the DOS in Fig. 2. They additionally show Ti $d$ derived DOS near and at $E_{\rm F}$, again similar to the DFT electronic structure. The similar peak positions and lack of satellite structures indicate that Pd$_2$TiIn is well described by standard DFT methods, and should not be considered as a strongly correlated material. This argues against strong correlations as the origin of the experimentally reported magnetic behavior of Pd$_2$TiIn. It furthermore supports the view that the Pd $d$ states are essentially occupied, meaning that magnetism associated with Pd will not occur in this compound, and therefore that Ti is the magnetically active element if there is any. We now turn to the Fermiology based on the results with the PBE functional at the experimental lattice parameter. The DOS at the Fermi level, $E_{\rm F}$ is $N(E_{\rm F})=3.64$ eV$^{-1}$ on a per formula unit both spins basis, including SOC. This value corresponds to a bare specific heat coefficient of $\gamma_{\rm bare}=8.6$ mJ/(mol$\cdot$f.u.$\cdot$K$^2$). It will be of interest to compare with experimental specific heat data to determine the enhancement $\lambda=\gamma/\gamma_{\rm bare}$, which may arise from spin fluctuations and or electron phonon coupling. The $d$ projections using a sphere radius of 2.5 bohr are 0.52 eV$^{-1}$ per Pd and 1.63 eV$^{-1}$ per Ti. Importantly, the Ti value does not reach the value of $\sim $$2.9$ eV$^{-1}$ per atom both spins that could be expected to lead to a Stoner instability towards ferromagnetism for Ti.[58] It may be noted that Stoner theory can be generalized to systems with several atoms and extended to finite moments.[59–61] However, regardless, magnetism is not expected if no site shows a sufficiently high projected DOS at $E_{\rm F}$ or averaged DOS as in the extended Stoner theory. This is the case here, and therefore no magnetism is anticipated within Stoner theory. The compound has three sheets of Fermi surface. These are shown in Fig. 3, based on calculations with the PBE functional, including SOC. They are hole surfaces, with an elongated character, around the $L$ points, a large sheet that intersects the zone boundary, and electron sheets at the $X$ point. The electron sheets at the $X$ point are from the lower of the two bands that intersect along $\varGamma$–$X$ forming the Dirac dispersion, and therefore the character of this sheet at the end along $\varGamma$–$X$ differs from that on the $X$-point face of the zone. The volumes enclosed by the Fermi surfaces are 0.009, 0.4857 and 0.0232 of the zone, for the three surfaces respectively, noting that the first is hole-like, and the others are given as electron-like. Note also that due to SOC in a centrosymmetric structure, each surface is two-fold degenerate. The different transport coefficients reflect details of the band shapes and provide useful experimental tests for theory.[62,63] The calculated Seebeck coefficient is small as expected for a metal, and positive, showing hole-like net behavior. The value at 300 K is 3.0 µV/K, while the value of $\sigma/\tau$ (the conductivity divided by the unknown scattering time), is $2.69\times 10^{20}$ $\Omega^{-1}$$\cdot$ms$^{-1}$.
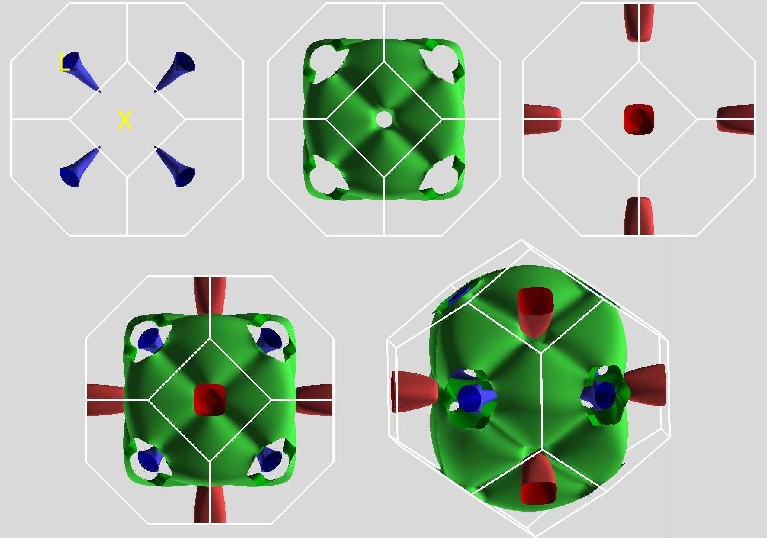
cpl-38-1-017102-fig3.png
Fig. 3. Fermi surface as obtained with the PBE functional including SOC. The top panel shows the small anisotropic $L$ centered hole pockets (blue), the large main sheet (green) and the small $X$ electron pockets (red). The bottom shows two views of the Fermi surface with all three sheets.
Disorder and Its Effect. It is known that site disorder can significantly change the magnetic behavior of some Heusler compounds. An example is Fe$_2$VAl where the ideal compound is likely paramagnetic and semimetallic, while site disorder introduces local moment behavior and unusual transport characteristics.[30–32] Furthermore, the magnetic behavior reported experimentally, in which a broad susceptibility maximum is seen rather than the characteristic shape of a phase transition suggests the possibility of disordered moments, possibly leading to spin glass behavior or weak magnetic ordering associated with these moments. This possibility is further suggested by the crystal chemical arguments mentioned above. We performed supercell calculations examining site disorder in order to address this possibility. These were carried out using 16 atom cells, consisting of the conventional unit cell, and were implemented with the PBE GGA. We constrained the lattice parameters to the experimental lattice parameter to facilitate comparisons but relaxed all internal atomic positions with no symmetry imposed. This was conducted using the forces in the LAPW method, including spin-polarization. We relaxed until the forces were all less than 1 mRy/Bohr. We begin with Ti antisite defects, where a Ti atom replaces either an In or a Pd atom. Both of these defects are strongly magnetic, with moments of 1.31$\mu_{\rm B}$ and 1.55$\mu_{\rm B}$, for Ti on an In and a Pd site, respectively. Importantly, this moment is distributed over the surrounding atoms, and not only on the Ti antisite atom. In the case of Ti on an In site, the near neighbor atoms are Pd. The moment on the Ti that is on the In site as measured in an LAPW sphere of radius 2.35 bohr, is only 0.12$\mu_{\rm B}$. The remainder of the moment occurs on one of the other Ti sites, specifically the Ti that is furthest from the antisite in the cell, which has a moment of 0.84$\mu_{\rm B}$, along with a small polarization distributed over the Pd atoms. The reason for the large polarization on the second neighbor Ti is structural. Replacement of In by Ti leads to a motion of the eight coordinating Pd towards the Ti antisite, with a short bond length of 2.61 Å, as compared to the ideal cubic structure, where it is 2.76 Å. This then leads to a motion of the Pd away from the second neighbor Ti, which has a longer bond length for its eight Pd neighbors of 2.90 Å. This longer bond length is then more favorable for moment formation. The induced moments are parallel to the moment on the Ti antisite. For the other case of Ti on a Pd site, we find a moment on the antisite Ti of 0.74$\mu_{\rm B}$, with the remaining moment distributed mainly over the four other Ti in the cell, also parallel to the moment on the antisite. Thus Ti antisites lead to moments.
Table 1. Energetics and calculated magnetic behavior for interchanges of atoms in the supercell (see text). $M$ denotes the total magnetization of the cell, and $m$ is the largest atomic moment on a Ti, as measured within an LAPW sphere of radius 2.35 bohr. Energies are relative to the ideal structure.
Configuration Energy (eV) M ($\mu_{\rm B}$/cell) $m$ ($\mu_{\rm B}$)
ideal 0 0.00 0.00
Pd$_{\rm In}$ In$_{\rm Pd}$ 1.21 0.00 0.00
Ti$_{\rm In}$ In$_{\rm Ti}$ 1.15 0.32 0.22
Ti$_{\rm Pd}$ Pd$_{\rm Ti}$ 1.08 1.39 0.67
We now turn to the energetics. In order to address this it is convenient to consider antisite pairs, which are exchanges of two atoms in the supercell. We considered three cases: (1) a Ti exchanged with an In, (2) a Ti exchanged with a Pd, and (3) a Pd exchanged with an In. The resulting energetics and moments are summarized in Table 1. As seen, antisite pairs in which a Ti is placed on another site lead to magnetic moments. It is possible that samples made experimentally have excess Ti, which would explain the magnetism. The energetics, where antisite pairs have energies near to but excess of 1 eV, suggest that while antisite defect formation is facile there may still not be sufficiently high concentrations of Ti antisites to explain the experimental observations unless there is excess Ti.
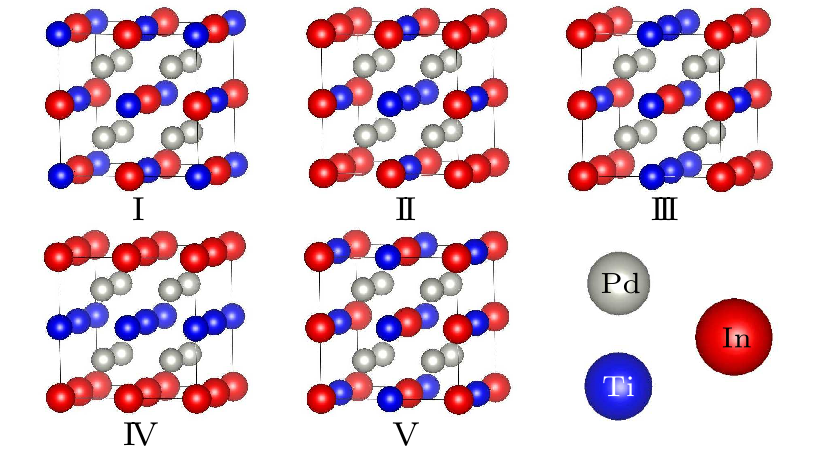
cpl-38-1-017102-fig4.png
Fig. 4. Supercell structures for the ideal structure (I) and structures with 50% swap disorder between Ti and In. The gray, cyan and purple spheres represent Pd, Ti, and In, respectively.
However, there is another possibility to consider, which is that disorder on the NaCl type, TiIn sublattice may be more favorable than the energetics of Table 1 suggest. The reason for this is that this is an ionic structure that may be stabilized by the Coulomb potential in the full Heusler crystal chemistry, and in that case large numbers of defects may be more stable than the expectation from the energetics of individual defects. In order to test this possibility we did supercell calculations with equal populations of Ti and In on the $B$ and $C$ sublattices of the $A_2BC$ full Heusler structure. These configurations are shown in Fig. 4. The corresponding energetics and magnetic properties are given in Table 2. The electronic densities of states are given in Fig. 5. All the configurations are metallic, and structures III and V, show spin-polarization.
Table 2. Energetics and calculated magnetic behavior cells with 50% swaps of Ti and In atoms (see text). The configurations correspond to Fig. 4. Energies and moments are for the 16-atom supercell (i.e. for 8 Pd and 4 Ti). Energies are relative to the ideal fully ordered Heusler structure. Here $M$ denotes the spin magnetization of the supercell, and $M_{\rm Pd}$ and $M_{\rm Ti}$ are the Pd and Ti contributions to it, respectively. In addition to the Pd and Ti moments, there is an interstitial component and a very small back polarization on the In sites.
Config. Energy (eV) $M$ ($\mu_{\rm B}$) $M_{\rm Pd}$ ($\mu_{\rm B}$) $M_{\rm Ti}$ ($\mu_{\rm B}$)
I (ideal) 0 0.00 0.00 0.00
II 0.24 0.00 0.00 0.00
III 1.15 0.64 0.06 0.48
IV 0.59 0.00 0.00 0.00
V 2.19 1.67 0.26 1.13
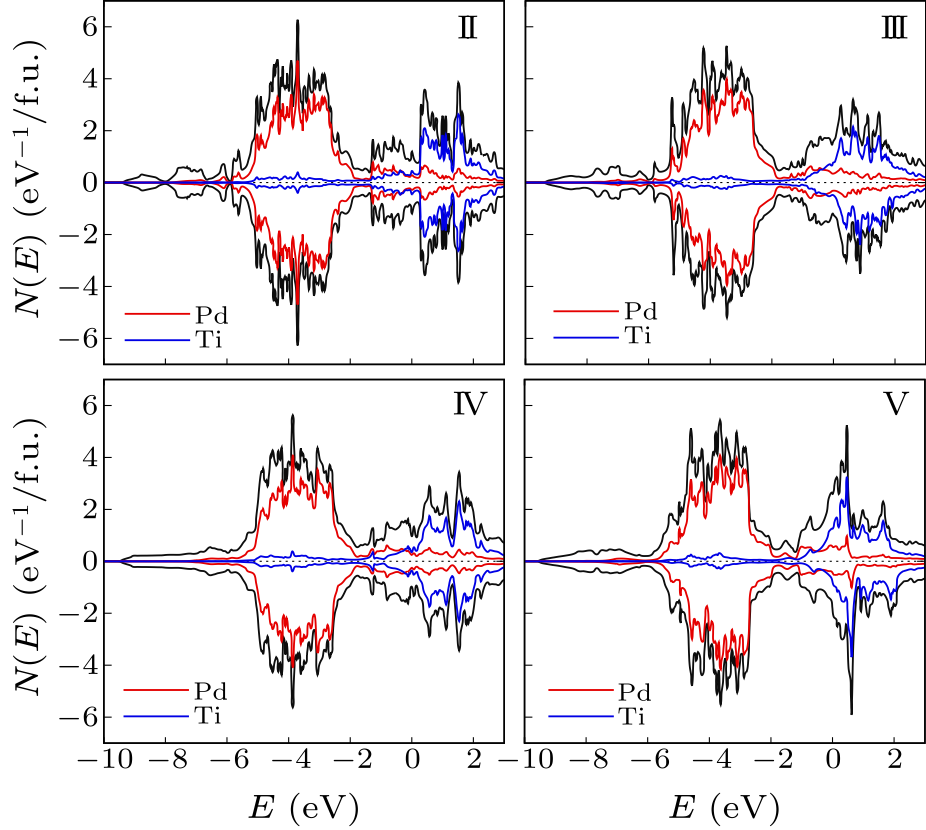
cpl-38-1-017102-fig5.png
Fig. 5. Electronic density of states for the structures II, III, IV and V, as shown in Fig. 4. These are on a per formula unit basis with majority spin shown as positive (above the axis) and minority spin as negative. The Pd and Ti projections are onto atom centered spheres of radius 2.35 Bohr.
While the ideal structure and lowest energy structures do not show moments, the two of higher energy structures do show moments. It is also noteworthy that structure III, which is formed from the ideal structure by two antisite pairs, has an energy only 1.15 eV above the ideal structure, which is comparable to the energy cost of a single antisite pair as given in Table 1. This suggests that indeed local disorder is likely in this compound and that this can lead to magnetism.
Table 3. PBE relaxed structure II for Pd$_2$TiIn. The structure II is cubic, spacegroup No. 221, $Pm\bar{3}m$, lattice parameter $a=6.50$ Å, $Z=4$.
Site $x$ $y$ $z$
Pd 8$g$ 0.2312 0.2312 0.7688
Ti1 3$d$ 0.5 0.0 0.0
Ti2 1$a$ 0.0 0.0 0.0
In1 1$b$ 0.5 0.5 0.5
In2 3$c$ 0.0 0.5 0.5
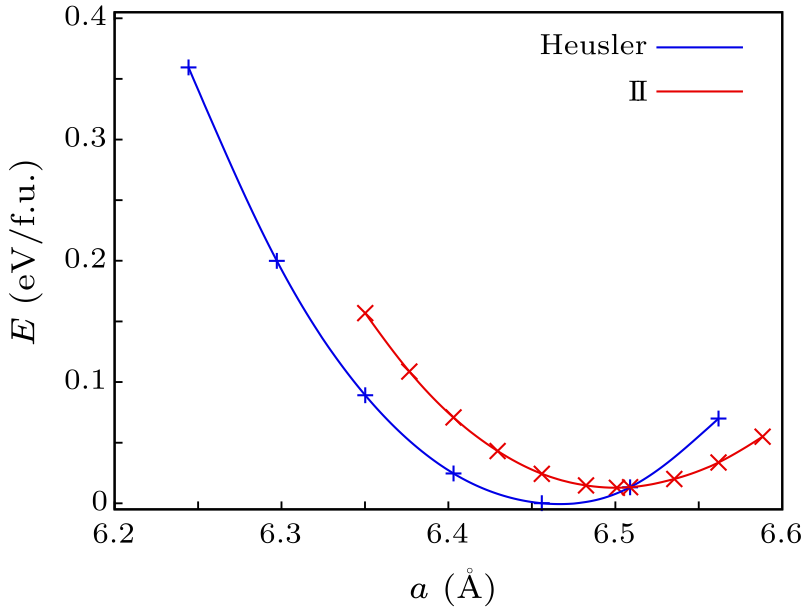
cpl-38-1-017102-fig6.png
Fig. 6. Energy as a function of lattice parameter as obtained with the PBE functional for the full Heusler structure and the new structure, II. Energies are per formula unit, with the energy zero as the lowest energy for the full Heusler structure.
A second noteworthy finding is that of the very low energy cost of structure II. This is 0.24 eV per 16-atom supercell above the ideal structure, or 1.4 kJ/mol atoms. This means that the structure II is practically degenerate in energy with the full Heusler structure and is very likely accessible by experiment. We note that it is a structure with a larger unit cell than the full Heusler structure, and therefore will have additional Bragg peaks, incompatible with the reported experimental diffraction data on existing samples.[25] Nonetheless, it will be of interest to examine whether this phase could be synthesized. In order to better characterize it we relaxed the lattice parameter using the PBE functional, and report structural parameters in Table 3. The energy as a function of lattice parameter in comparison with the normal full-Heusler structure is given in Fig. 6. The $Pm\overline{3}m$ structure has Ti at Wycoff positions 1$a$ and 3$d$, i.e., (0,0,0), ($\frac{1}{2}$,0,0), (0,$\frac{1}{2}$,0) and (0,0,$\frac{1}{2}$), In at 3$c$ and 1$b$, i.e. (0,$\frac{1}{2}$,$\frac{1}{2}$), ($\frac{1}{2}$,0,$\frac{1}{2}$), ($\frac{1}{2}$,$\frac{1}{2}$,0) and ($\frac{1}{2}$,$\frac{1}{2}$,$\frac{1}{2}$) and Pd at 8$g$, i.e., ($\pm x$,$\pm x$,$\pm x$). Thus Pd is along lines between the Ti at the corner and In at the body center. It is displaced to be closer to Ti than In ($x$ depends on volume, and is 0.2312 at $a=6.50$ Å. Differences between structure II and the ideal full Heusler structure are that structure II is less favorable for an ionic arrangement of In and Ti atoms, but is better able to accommodate the different sizes of these atoms. In particular, for the PBE relaxed full Heusler structure, with $a=6.46$ Å, the Ti–Pd and In–Pd distances are both 2.80 Å. For the relaxed $Pm\bar{3}m$ structure II, $a=6.50$ Å, the Ti–Pd distances are significantly shorter than the In–Pd distances. Specifically, Ti1 is coordinated by eight Pd at 2.75 Å, and Ti2 is coordinated by eight Pd at 2.60 Å. Meanwhile In1 has eight Pd neighbors at 3.03 Å, and In2 has eight Pd neighbors at 2.89 Å. In any case, structure II is not found to be magnetic. This is the case both at the experimental lattice parameter of full Heusler Pd$_2$TiIn and at the relaxed PBE lattice parameter for structure II. However, this low energy competing structure, which differs in the ordering on the In–Ti sites, indicates that a substantial amount of disorder can be expected in samples, and the other results suggest that this can lead to magnetic behavior. Besides antisite defects, it is also possible that vacancies may play a role in the properties. For example, Pd vacancies were proposed as a way of modifying the band structure of Pd$_2$TiSn, with compositions intermediate between the full Heusler and the half-Heusler PdTiSn.[64] We considered vacancies on each of the three sites, using the same supercell method as for the antisite pairs discussed above. Vacancy formation energies were calculated with respect to bulk Pd, Ti and In metal in their experimental crystal structures, specifically fcc Pd, hcp Ti and body centered tetragonal In. The vacancy formation energies thus obtained were 1.25 eV for $V_{\rm Pd}$, 1.53 eV for $V_{\rm Ti}$, and 1.47 eV for $V_{\rm In}$. Neither Pd nor Ti vacancies yielded moments. However, one of the Ti atoms in the supercell with an In vacancy develops a moment, leading to a total magnetization of the In vacancy containing supercell of 1.13$\mu_{\rm B}$ in that case. The mechanism for moment formation is similar to that discussed above for antisites. Specifically, the Pd atoms around the In vacancy move inwards and towards the vacancy. This means that they move away from one of the Ti atoms in the supercell. The Ti–Pd bond lengths for this atom increase to 2.98 Å, as compared to the original value of 2.76 Å. This reflects the usual competition between bonding, with paired electrons, and magnetism with unpaired electrons. Nonetheless, it is interesting to observe that it leads to magnetism in defected Pd$_2$TiIn. In conclusion, first principles calculations of the electronic and magnetic properties of full Heusler Pd$_2$TiIn show that it is a paramagnetic metal, with an electronic structure showing a moderately high DOS at the Fermi level derived from Ti $d$ states. This itinerant behavior means that moments from Curie–Weiss fitting as has been reported may not represent actual values of local moments on atoms. The Pd $d$ states are nearly fully occupied in accord with existing photoemission data. This means that Pd moments are unlikely. Furthermore, we do not find magnetism in this compound with either the PBE or LDA functionals. However, defects in which Ti occurs on either In or Pd sites do lead to moment formation, as well as polarization of other neighboring transition element atoms, parallel to the moment on the Ti defect. We also find that vacancies on the In sites can lead to magnetic moments on Ti atoms. These results are seemingly in accord with the magnetic behavior observed experimentally in which a broad maximum in susceptibility is seen but no clear ordering is detected. In particular, it suggests a glassy behavior that may be associated with disorder, provided that a sufficient number of defects is present. Also, it means that the magnetic behavior may be influenced by synthesis conditions, for example the presence of excess Ti, In deficiency, or synthesis temperatures and annealing conditions. It will be of interest to further examine the dependence of magnetic behavior on synthesis conditions in experiments. In addition, we find that there is an alternative structure for Pd$_2$TiIn that is very close in energy to the ordered full-Heusler structure. This cubic phase is a non-ferromagnetic metal. It will be of interest to search for this phase by experiments, and investigate its properties if found. References Simple rules for the understanding of Heusler compoundsCalculated electronic and magnetic properties of the half-metallic, transition metal based Heusler compoundsHeusler compounds and spintronicsDirect observation of half-metallicity in the Heusler compound Co2MnSiSpin polarization of Co2FeSi full-Heusler alloy and tunneling magnetoresistance of its magnetic tunneling junctionsMagnetic order in Pd2TiIn: A new itinerant antiferromagnet?Co2MnSi Heusler alloy as magnetic electrodes in magnetic tunnel junctionsProperties of the quaternary half-metal-type Heusler alloy Co 2 Mn 1 − x Fe x Si Realization of Spin Gapless Semiconductors: The Heusler Compound Mn 2 CoAl First-principles calculation of the intersublattice exchange interactions and Curie temperatures of the full Heusler alloys Ni 2 Mn X ( X = Ga , In , Sn , Sb ) Magnetic and half-metallic properties of new Heusler alloys Ru2MnZ (Z  Si, Ge, Sn and Sb)Slater–Pauling behavior and half-metallicity in Heusler alloys Mn2CuZ (Z=Ge and Sb)Magnetic and transport properties of the rare-earth-based Heusler phases R Pd Z and R Pd 2 Z ( Z = Sb , Bi ) Interplay of local moment and itinerant magnetism in cobalt-based Heusler ferromagnets: Co 2 TiSi ,   Co 2 MnSi and Co 2 FeSi Type-II Dirac states in full Heusler compounds X InPd 2 ( X = Ti, Zr, and Hf)Thermoelectric performance of a metastable thin-film Heusler alloyObservation of enhanced thermopower due to spin fluctuation in weak itinerant ferromagnetFerromagnetism in an intermetallic compound containing palladium, titanium and aluminiumPd2TiAl: investigated by monochromatic, circularly polarized Mössbauer sourceDensity of States in Ordered and Disordered Pd2TiAl and Pd2TiSn Heusler AlloysMagnetic order in ternary intermetallic compounds containing palladium and titaniumThe experimental density of states of Pd 4d and Ti 3d in the intermetallic compoundElectronic Structure and Magnetic Properties of Intermetallic AlloysA neutron diffraction study of the phase transition in Pd 2 TiInIs ThInPd2 magnetic?Electronic structure in ternary intermetallic Pd 2 TiX (X=Al,Ga,In) Heusler-type alloys: are they magnetic?Bioactive Natural Products from Endophytic MicrobesQuantum critical point and ferromagnetic semiconducting behavior in p -type FeAs 2 Electronic structure, local moments, and transport in Fe 2 VAl Physical properties of Heusler-like Fe 2 VAl Electronic and thermoelectric properties of Fe 2 VAl: The role of defects and disorderWIEN2k: An APW+lo program for calculating the properties of solidsGround-state properties of lanthanum: Treatment of extended-core statesAn alternative way of linearizing the augmented plane-wave methodGeneralized Gradient Approximation Made SimpleBoltzTraP. A code for calculating band-structure dependent quantitiesGeneralized Slater-Pauling rule for the inverse Heusler compounds171 Scandium-based full Heusler compounds: A comprehensive study of competition between XA and L21 atomic orderingUltralow Thermal Conductivity in Full Heusler SemiconductorsThermoelectric high ZT half-Heusler alloys Ti1−x−yZrxHfyNiSn (0 ≤ x ≤ 1; 0 ≤ y ≤ 1)Discovery of TaFeSb-based half-Heuslers with high thermoelectric performanceCharge carrier concentration optimization of thermoelectric p -type half-Heusler compoundsCharacterization of rattling in relation to thermal conductivity: Ordered half-Heusler semiconductorsSoft-mode enhanced type-I superconductivity in LiP d 2 Ge Atomic Radii and Interatomic Distances in MetalsItinerant metamagnetism in YCO 2Density-functional study of Fe 3 Al : LSDA versus GGADensity functional methods for the magnetism of transition metals: SCAN in relation to other functionalsMagnetism, critical fluctuations, and susceptibility renormalization in PdCompeting magnetic orders in quantum critical Sr 3 Ru 2 O 7 Electron-energy-loss spectra and the structural stability of nickel oxide:??An LSDA+U studyLinear response approach to the calculation of the effective interaction parameters in the LDA + U methodApplication of screened hybrid functionals to the bulk transition metals Rh, Pd, and PtA photoemission investigation of the valence band electronic structure of andUniform susceptibilities of metallic elementsMetamagnetic behavior of fcc ironMagnetic ground state properties of transition metalsElectronic structure and magnetism in Ru-based perovskitesPhase transitions in LaFeAsO: Structural, magnetic, elastic, and transport properties, heat capacity and Mössbauer spectraLorenz number in relation to estimates based on the Seebeck coefficientEffect of vacancies on the electronic structure of Pd x TiSn alloys
[1]Heusler F 1903 Verhandlungen Deutschen Physikalischen Ges. 5 219
[2] Graf T, Felser C and Parkin S S P 2011 Prog. Solid State Chem. 39 1
[3] Kandpal H C, Fecher G H and Felser C 2007 J. Phys. D 40 1507
[4] Palmstrom C J 2016 Prog. Cryst. Growth Charact. Mater. 62 371
[5] Jourdan M, Minar J, Braun J, Kronenberg A, Chadov S, Balke B, Glskovskii A, Kolbe M, Elmers H J, Schonhense G, Ebert H, Felser C and Klaui M 2014 Nat. Commun. 5 3974
[6] Gersci Z, Rajanikanth A, Takahashi Y K, Hono K, Kikuchi M, Tezuka N and Inomata K 2006 Appl. Phys. Lett. 89 082512
[7] Neumann K U, Crangle J, Kremer R K, Zayer N K and Ziebeck K R A 1993 J. Magn. Magn. Mater. 127 47
[8] Kämmerer S, Thomas A, Hütten A and Reiss G 2004 Appl. Phys. Lett. 85 79
[9] Balke B, Fecher G H, Kandpal H C, Felser C, Kobayashi K, Ikenaga E, Kim J J and Ueda S 2006 Phys. Rev. B 74 104405
[10] Ouardi S, Fecher G H, Felser C and Kübler J 2013 Phys. Rev. Lett. 110 100401
[11] Şaşıoğlu E, Sandratskii L M and Bruno P 2004 Phys. Rev. B 70 024427
[12] Ishida S, Kashiwagi S, Fujii S and Asano S 1995 Physica B 210 140
[13] Luo H, Liu G, Meng F, Wang L, Liu E, Wu G, Zhu X and Jiang C 2011 Comput. Mater. Sci. 50 3119
[14] Gofryk K, Kaczorowski D, Plackowski T, Leithe-Jasper A and Grin Y 2005 Phys. Rev. B 72 094409
[15] Qin G, Ren W and Singh D J 2020 Phys. Rev. B 101 014427
[16] Mondal C, Barman C K, Pathak B and Alam A 2019 Phys. Rev. B 100 245151
[17] Hinterleitner B, Knapp I, Poneder M, Shi Y, Muller H, Eguchi G, Eisenmenger-Sittner C, Stoger-Pollach M, Kakefuda Y, Kawamoto N, Guo Q, Baba T, Mori T, Ullah S, Chen X Q and Bauer E 2019 Nature 576 85
[18] Tsujii N, Nishide A, Hayakawa J and Mori T 2019 Sci. Adv. 5 eaat5935
[19] Neumann K U, Crangle J, Smith J G and Ziebeck K R A 1994 J. Magn. Magn. Mater. 137 264
[20] Szymanski K, Biernacka M, Dobrzynski L, Neumann K U, Perzynska K, Satula D, Zaleski P and Ziebeck K R A 1999 J. Magn. Magn. Mater. 195 651
[21] Jezierski A 1995 Phys. Stat. Sol. (b) 190 471
[22] Neumann K U, Crangle J, Smith J G, Zayer N K and Ziebeck K R A 1995 J. Magn. Magn. Mater. 140 185
[23] Liddiard A J, Brown D, Crapper M D, Petty M, Smith J G, Telling N D, Bedwell K H, Flannery L B and Skull P A 1996 J. Phys.: Condens. Matter 8 3955
[24] Jezierski A, Pugacheva M, Morkowski J A and Szajek A 1997 Acta Phys. Pol. A 91 151
[25] Ouladdiaf B, Neumann K U, Crangle J, Zayer N K, Ziebeck K R A and Ressouche E 1994 J. Phys.: Condens. Matter 6 1563
[26] Jaswal S S 1995 J. Magn. Magn. Mater. 139 L1
[27] Jezierski A, Morkowski J A, Szajek A and Pugacheva M 1995 J. Phys.: Condens. Matter 7 4447
[28] Zhang Q, Ren Z, Wu N, Wang W, Gao Y, Zhang Q, Shi J, Zhuang L, Sun X and Fu L 2018 npj 2D Mater. Appl. 2 22
[29] Lei B H, Fu Y, Feng Z and Singh D J 2020 Phys. Rev. B 101 020404(R)
[30] Singh D J and Mazin I I 1998 Phys. Rev. B 57 14352
[31] Feng Y, Rhee J Y, Wiener T A, Lynch D W, Hubbard B E, Sievers A J, Schlagel D L, Lograsso T A and Miller L L 2001 Phys. Rev. B 63 165109
[32] Bilc D I and Ghosez P 2011 Phys. Rev. B 83 205204
[33]Singh D J and Nordstrom L 2006 Planewaves Pseudopoten-tials and the LAPW Method 2nd edn (Berlin: Springer)
[34] Blaha P, Schwarz K, Tran F, Laskowski R, Madsen G K H and Marks L D 2020 J. Chem. Phys. 152 074101
[35] Singh D 1991 Phys. Rev. B 43 6388
[36] Sjostedt E, Nordstrom L and Singh D J 2000 Solid State Commun. 114 15
[37] Perdew J P, Burke K and Ernzerhof M 1996 Phys. Rev. Lett. 77 3865
[38] Madsen G K H and Singh D J 2006 Comput. Phys. Commun. 175 67
[39] Skaftouros S, Ozdogan K, Sasioglu E and Galanakis I 2013 Phys. Rev. B 87 024420
[40] Han Y, Chen Z, Kuang M, Liu Z, Wang X and Wang X 2019 Results Phys. 12 435
[41] He J, Amsler M, Xia Y, Naghavi S S, Hegde V I, Hao S, Goedecker S, Ozolins V and Wolverton C 2016 Phys. Rev. Lett. 117 046602
[42] Gurth M, Rogl G, Romaka V V, Grytsiv A, Bauer E and Rogl P 2016 Acta Mater. 104 210
[43] Zhu H, Mao J, Li Y, Sun J, Wang Y, Zhu Q, Song Q, Zhou J, Fu Y, He R, Tong T, Liu Z, Ren W, Wang Z, Luo J, Sotnikov A, Bao J, Nielsch K, Chen G, Singh D J and Ren Z 2019 Nat. Commun. 10 270
[44] Rausch E, Balke B, Deschauer T, Ouradi S and Felser C 2015 APL Mater. 3 041516
[45] Feng Z, Fu Y, Zhang Y and Singh D J 2020 Phys. Rev. B 101 064301
[46] Gornicka K, Kuderowicz G, Carnicom E M, Kutorasinski K, Wiendlocha B, Cava R J and Klimczuk T 2020 Phys. Rev. B 102 024507
[47] Pauling L 1947 J. Am. Chem. Soc. 69 542
[48] Schwarz K and Mohn P 1984 J. Phys. F 14 L129
[49] Lechermann F, Welsch F, Elsasser C, Ederer C, Fahnle M, Sanchez J M and Meyer B 2002 Phys. Rev. B 65 132104
[50] Fu Y and Singh D J 2019 Phys. Rev. B 100 045126
[51]Moriya T 1985 Spin Fluctuations in Itinerant Electron Magnetism (Berlin: Springer)
[52] Larson P, Mazin I I and Singh D J 2004 Phys. Rev. B 69 064429
[53] Putatunda A, Qin G, Ren W and Singh D J 2020 Phys. Rev. B 102 014442
[54] Dudarev S L, Botton G A, Savrasov S Y, Humphreys C J and Sutton A P 1998 Phys. Rev. B 57 1505
[55] Cococcioni M and de Gironcoli S 2005 Phys. Rev. B 71 035105
[56] Tran F, Koller D and Blaha P 2012 Phys. Rev. B 86 134406
[57] Brown D, Crapper M D, Bedwell K H, Petty M, Smith J G and Telling N D 1997 J. Phys.: Condens. Matter 9 2955
[58] Janak J F 1977 Phys. Rev. B 16 255
[59] Krasko G L 1987 Phys. Rev. B 36 8565
[60] Andersen O K, Madsen J, Poulsen U K, Jepsen O and Kollar J 1977 Physica B+C 86 249
[61] Mazin I I and Singh D J 1997 Phys. Rev. B 56 2556
[62] McGuire M A, Christianson A D, Sefat A S, Sales B C, Lumsden M D, Jin R, Payzant E A, Mandrus D, Luan Y, Keppens V, Varadarajan V, Brill J W, Hermann R P, Sougrati M T, Grandjean F and Long G J 2008 Phys. Rev. B 78 094517
[63] Putatunda A and Singh D J 2019 Mater. Today Phys. 8 49
[64] Jezierski A 2000 J. Phys.: Condens. Matter 12 8127