⇦Chinese Physics Letters, 2019, Vol. 36, No. 6, Article code 061201 Predictions of the Chou–Yang Model for p-p Scattering at $\sqrt s =8$ TeV S. Zahra1**, H. Rashid2 Affiliations 1Department of Physics DS&T, University of Education, Lahore, Pakistan 2Government College Women University, Sialkot, Pakistan Received 17 August 2018, online 18 May 2019 **Corresponding author. Email: sarwat.zahra@ue.edu.pk Citation Text: Zahra S and Rashid H 2019 Chin. Phys. Lett. 36 061201    Abstract At low four-momentum transfer squared $0.02 < -t < 0.2$ (GeV/$c$)$^{2}$, we use the Chou–Yang model to predict the form factor of protons from proton–proton elastic scattering at center-of-mass energy $\sqrt s=8$ TeV. By fitting differential cross-sectional data from the TOTEM experiment to a single Gaussian, the form factor is extracted. We use this form factor to find the rms matter radius of the proton to be 0.88 fm, which is in good agreement with the experimental data and the theoretically predicted values of the rms radius. DOI:10.1088/0256-307X/36/6/061201 PACS:12.90.+b, 14.20.Dh, 13.40.Gp © 2019 Chinese Physics Society Article Text Exploration of fundamental particles and their interactions is the soul of particle physics. Information in this regard can be provided by the study of hadronic matter. To investigate the unclear picture of hadronic matter, experimental studies are being undertaken by several experimental groups, such as TOTEM,[1]. At CERN the TOTEM experiment is a long way from probing the structure of the proton, which is still an open problem. In our work, the computation of rms radii is carried out through electromagnetic form factors obtained by the Chou–Yang model to probe the structure of the proton. In the geometrical model, primarily, the two hadrons are considered to be elastically scattered. In these models, hadrons are considered to be relatively translucent objects going through each another without any attenuation. Here, we commonly have two measuring quantities in such studies of scattering processes, i.e., the differential cross-section and total cross-section. The differential cross-section is related to the matter distribution in the hadrons. The total cross-section is related to the size of a hadron. The logarithmic increase was observed in the total cross-section with the increase of the incoming energy of scattering hadrons. This rise in the total cross-section provides us two possibilities for a geometrical model/picture: (i) The increase of the incoming energy does not alter the matter distribution or size of a hadron. Therefore, in this case, with increasing the incoming energy of colliding hadrons there is an increase in the total cross-section, which is responsible for the increase in their opaqueness or the interaction strength. (ii) The total cross-section increases due to the increase in the size of colliding hadrons. Clark and Lo[2] discussed the energy dependence of the elastic cross-section at high energies. In 1974 Buras and Dias[3] gave their hypothesis about geometrical scaling by considering the second choice. On the other hand, the Chou–Yang model[4] is an illustration of the first option. In the Chou–Yang model, the matter distribution within a hadron is supposed to be identical to the charge distribution in it. By definition the charge distribution can only be a function of squared four-momentum transfer, thus it cannot be a function of energy. Such observation was made in the measurements of the form factor of the proton in electromagnetic current that is found to be a function of only squared momentum transfer. A change in the matter distribution cannot be considered to be accountable for the energy dependence of the total cross-section. Thus distinguishing both the prospects in the geometrical model of hadrons would expose a vibrant image. It was pointed out in 1973 by Chou and Yang[5] that their model is consistent with the results of proton–proton scattering at ISR by CERN. Lo and Lai[6] in 1977 studied a few analytical models explaining data on greater energies, which will be accessible in future experiments, and they found that the dependence of the total cross-section on the energy can be attributed to the change in the distribution of matter at asymptotic energies. Before moving towards the Chou–Yang model, the importance of form factors should be highlighted.[7] The matter distribution in space is related to the form factor. For the same reason, matter distribution inside a hadron is related to the hadronic form factor. Scattering experiments can directly give us the form factors. We can obtain the hadronic form factor through either elastic scattering of two hadrons or in the scattering processes of hadrons and electrons. Among all the hadrons, nucleons are readily accessible, therefore the p-p elastic scattering experiment is easier to perform. It is explained in Ref.  [7], where two hadrons A and B are considered. The product of their form factors using the Chou–Yang model is given by $$\begin{align} &F_{\rm A} (t)F_{\rm B} (t)\\ =\,&{\rm constant}\Big[a_{\rm AB} (t)+\frac{a_{\rm AB} (t)\ast a_{\rm AB} (t)}{2} \\ &+\frac{a_{\rm AB}(t)\ast a_{\rm AB} (t)\ast a_{\rm AB} (t)}{3}+\ldots\Big],~~ \tag {1} \end{align} $$ where $a_{\rm AB}(t)$ represents the asymptotic scattering amplitude for the A+B$\to$A+B scattering process. We can acquire the direct numerical values for the scattering amplitude by following the above relation, i.e., $a_{\rm AB}(t)=({\frac{1}{\pi}\frac{d\sigma}{dt}})^{1/2}$. As $a_{\rm AB}(t)$ acquires the numerical value, $\ast$ is ordinary multiplication here. Now by considering the situation, a Gaussian (in $t$) could be used to approximate the differential cross-section. In that particular case the differential cross-section is written as $\frac{d\sigma}{dt}=\alpha e^{\beta t}$. Considering Eq. (1) and from only the first term on the right-hand side, the product of the form factor can be obtained approximately as $$\begin{align} F_{\rm A}(t)F_{\rm B}(t)\cong e^{(\frac{\beta}{2})t}.~~ \tag {2} \end{align} $$ Hadron's radius is associated with the form factor by $$\begin{align} F_{\rm A} (t)=1-\frac{1}{6}t\langle {r^{2}} \rangle +\cdots.~~ \tag {3} \end{align} $$ Using Eqs. (2) and (3), it is found that there is a relation between the radii of both the hadrons, i.e., $$\begin{align} \langle {r_{\rm A}^{2}} \rangle +\langle {r_{\rm B}^{2}} \rangle \cong 3\beta.~~ \tag {4} \end{align} $$ However, if we consider the hadrons to be at a point of $r\approx 0$, this will lead to $\beta \approx 0$. Thus there will be a very flat distribution of the differential cross-section of hadrons, while a sharp slope in the differential cross-section is an indication of larger hadrons. The value of $\beta$ used typically in the experiments is 10 GeV$^{-2}$. By considering entire terms on the right-hand side of Eq. (1), the product of both form factors ($F_{\rm A}(t)$ and $F_{\rm B}(t)$) of two hadrons (A and B) turns out to be $$\begin{alignat}{1} F_{\rm A} (t)F_{\rm B} (t)=\,&{\rm constant}\\ &\times \sum\limits_{n=1}^\infty {\frac{1}{n}} \Big({\frac{\alpha}{\pi}}\Big)^{n/2}\Big({\frac{1}{\beta}}\Big)^{n} \frac{\beta}{n}e^{\beta t/2n}.~~ \tag {5} \end{alignat} $$ It is clear that a Gaussian differential cross-section is produced by form factors that drop off much less than a Gaussian curve, thus in that special case the differential cross-section is known as the Gaussian differential cross-section. Accordingly, the radii of the two scattering hadrons are related to each other in terms of $\alpha$ and $\beta$ and are given by $$\begin{align} \langle {r_{\rm A}^{2}} \rangle +\langle {r_{\rm B}^{2}} \rangle =\frac{6\sum\limits_{n=1}^\infty {\frac{1}{n}({\frac{\alpha}{\pi}})^{n/2}( {\frac{1}{\beta}})^{n}\frac{\beta^{2}}{2n^{2}}}}{\sum\limits_{n=1}^\infty {\frac{1}{n}({\frac{\alpha}{\pi}})^{n/2}({\frac{1}{\beta}})^{n}\frac{\beta}{n}}},~~ \tag {6} \end{align} $$ which is very useful to compute the radii of scattering hadrons by fitting the differential cross-section in a single Gaussian. In our work, we have used the data of elastic proton–proton scattering at $\sqrt s =8$ TeV from TOTEM.[1] By fitting the experimental data to a single Gaussian (Fig. 1), we have found the most appropriate values of $\alpha$ and $\beta$ to be equal to $531.95\,\frac{{\rm mb}^{{\rm -1}}}{{\rm GeV}}{\rm /c}$ and $-19.53\,({\rm GeV})^{-2}$, respectively. These values of $\alpha$ and $\beta$ have been used in Eq. (5) directly. Using a computer program, this equation has been solved for finite values of $n$. In this way, the form factor of protons has been obtained, which is found to be equal to $$\begin{align} F_{\rm P} =\,&0.23\times (0.10e^{-48.84t}-0.24e^{-39.07t} \\ &+0.64e^{-29.30t}-2.17e^{-19.53t}\\ &+13.01e^{-9.77t})^{1/2}.~~ \tag {7} \end{align} $$
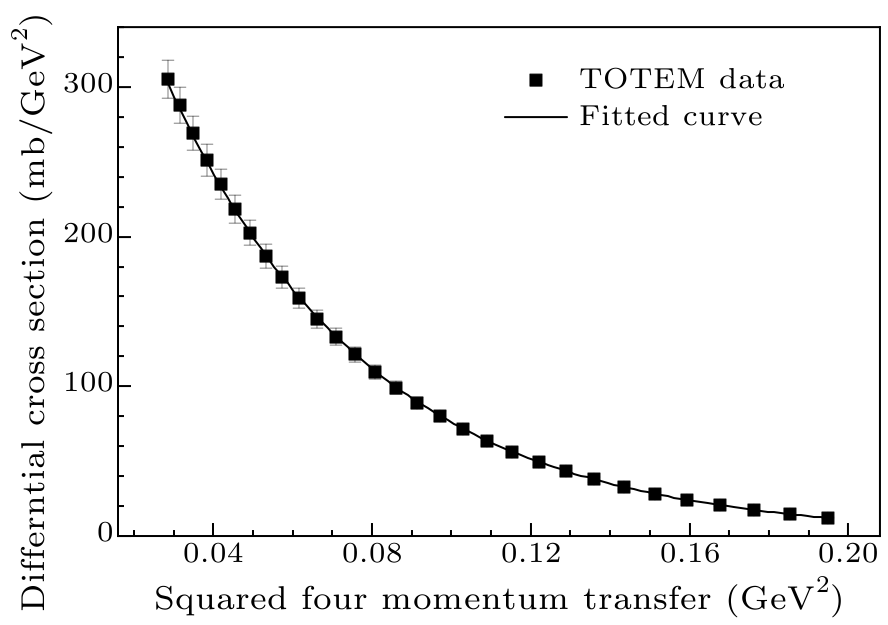
cpl-36-6-061201-fig1.png
Fig. 1. Single Gaussian fitting of differential cross-section data of proton–proton scattering at $\sqrt s =8$ TeV.
Using the form factor from Eq. (7) we can directly compute the rms radius of the proton using the following relation, $\langle {r^{2}} \rangle =-6\eta^{2}{\frac{dF(t)}{dt}}|_{t=0}$. We have therefore computed the value of $\langle {r_{\rm P}} \rangle =0.888$ fm, which is in good agreement with the experimental data ($\langle {r_{\rm P}} \rangle =0.841$ fm,[8] $\langle {r_{\rm P}} \rangle =0.876$ fm[9]) as well as that predicted from the theoretical models (for the Toy model $\langle {r_{\rm P}} \rangle =0.801$ fm,[10] $\langle {r_{\rm P}} \rangle =0.807$ fm[11]). The Chou–Yang model has excellent predicting power for the elastic scattering process at lower and higher values of $\sqrt s$. At low squared momentum transfer, i.e., $0.02 < -t < 0.2$ (GeV/$c$)$^{2}$, we can find good results of the form factor even at a high center-of-mass energy of $\sqrt s=8$ TeV by fitting the experimental data to a single Gaussian. Figure 1 shows a graph of the experimental data from TOTEM[1] (represented by dots), in which the solid line shows our fit. We have found the most appropriate fit at $0.02 < -t < 0.2$ (GeV/$c$)$^{2}$. It is not applicable for higher values of squared momentum transfer. The generalized Chou–Yang model[12] will be presented later to explain the experimental data which are outside the region of the diffraction peak. References Evidence for non-exponential elastic proton–proton differential cross-section at low | t | and s = 8 TeV by TOTEMShift of peaks and dips in elastic scattering in the Chou-Yang modelScaling law for the elastic differential cross section in pp scattering from geometric scalingModel of Elastic High-Energy ScatteringOpaqueness of pp Collisions from 30 to 1500 GeV/ cStudy of the energy dependence in geometrical modelsThe size of the protonCODATA recommended values of the fundamental physical constants: 2006Muonic hydrogen and the third Zemach momentOn the rms-radius of the proton
[1] Antchev G et al 2015 Nucl. Phys. B 899 527
[2] Clark D J and Lo S Y 1974 Phys. Rev. D 10 1519
[3] Buras A J and Deus J D 1974 Nucl. Phys. B 71 481
[4] Chou T T and Yang C N 1968 Phys. Rev. 170 1591
[5] Chao A W and Yang C N 1973 Phys. Rev. D 8 2063
[6] Lo S Y and Lai C S 1977 J. Phys. G 3 465
[7]Shui-Yin Lo 1987 Geometrical Pictures in Hadronic Collisions: A Reprint Volume (Singapore: World Scientific) chap 4 p 37
[8] Pohl K et al 2010 Nature 466 213
[9] Mohr P J et al 2008 Rev. Mod. Phys. 80 633
[10] Friar J L and Sick I 2005 Phys. Rev. A 72 040502
[11] Sick I 2003 Phys. Lett. B 576 62
[12]Aleem F and Ali S 1991 IAEA Hadronic J. 14 173