⇦Chinese Physics Letters, 2017, Vol. 34, No. 2, Article code 026402Express Letter Intrinsic Features of an Ideal Glass * Deyan Sun(孙得彦)1,3, Cheng Shang(商城)2, Zhipan Liu(刘智攀)2, Xingao Gong(龚新高)3,4** Affiliations 1Department of Physics, East China Normal University, Shanghai 200062 2Department of Chemistry, Fudan University, Shanghai 200433 3Key Laboratory for Computational Physical Sciences (MOE), State Key Laboratory of Surface Physics, Department of Physics, Fudan University, Shanghai 200433 4Collaborative Innovation Center of Advanced Microstructures, Nanjing 210093 Received 22 January 2017 *Supported by the National Natural Science Foundation of China, and the National Basic Research Program of China.
**Corresponding author. Email: xggong@fudan.edu.cn Citation Text: Sun D, Shang C, Liu Z and Gong X 2017 Chin. Phys. Lett. 34 026402 Abstract In order to understand the long-standing problem of the nature of glass states, we perform intensive simulations on the thermodynamic properties and potential energy surface of an ideal glass. It is found that the atoms of an ideal glass manifest cooperative diffusion, and show clearly different behavior from the liquid state. By determining the potential energy surface, we demonstrate that the glass state has a flat potential landscape, which is the critical intrinsic feature of ideal glasses. When this potential region is accessible through any thermal or kinetic process, the glass state can be formed and a glass transition will occur, regardless of any special structural character. With this picture, the glass transition can be interpreted by the emergence of configurational entropies, as a consequence of flat potential landscapes. DOI:10.1088/0256-307X/34/2/026402 PACS:64.70.pe, 61.43.Fs, 61.20.Ja, 65.80.-g © 2017 Chinese Physics Society Article Text The nature of glassy states (GSs) is one of the most compelling puzzles and questions facing scientists today.[1] The significance of GS not only lies in the importance of their various applications, but also stems from the challenge to current theories in condensed matter physics and thermodynamics.[2,3] Until now, it is probably safe to say that both GSs and the glass transition (GT) are within a dark area in the field of materials science and condensed matter physics. Given that a glass is neither a normal liquid nor a standard solid, GSs are quite often not described in any detail by standard textbooks.[4] Although the problems have been recognized over a century and great efforts have been made on various aspects of GSs and GT, from disordered structures to kinetic fragility, from dynamic heterogeneity to thermodynamic models,[4-8] the debate on essential issues is still quite lively. One of most crucial issues regarding GS is that below the Kauzmann temperature $T_{\rm K}$ the entropy of a supercooled liquid by extrapolation becomes lower than the crystal entropy.[9] This constitutes the so-called Kauzmann paradox the thermodynamic models face. To avoid the paradox, an unusual state of matter, namely an ideal glass, was proposed.[10-13] It is defined as a glass state with zero configurational entropy. For more than half a century, the ideal glass remained a conjecture, as its existence has been doubtful in real materials.[14] In 1998, two of the present authors (DY and XG) demonstrated that an Al$_{43}$ cluster in its most stable configuration shows a typical glass transition character,[15] which can be identified as an ideal glass.[16] Ten years later, the ideal glass was found experimentally in that system.[17] To our knowledge, the Al$_{43}$ cluster may be the first ideal glass theoretically predicted in real materials. It thus provides an ideal system to study the nature of the GS and GT at the atomic level. In this Letter, we report the results of molecular dynamics (MD) simulations and stochastic surface walking (SSW)[18,19] studies of the thermodynamic properties of the ideal glass Al$_{43}$. For comparison, the symmetric Al$_{55}$ with $I_h$ symmetry and Al$_{40}$ with $D_{6h}$ symmetry are also studied.[20] The SSW algorithm was recently developed by Shang and Liu and has been proven to be an efficient tool to explore the potential landscape of both clusters and periodic systems.[21,22] An automated climbing mechanism is implemented in the SSW algorithm to manipulate a structural configuration from a local minimum to a high-energy configuration along one random mode direction. We find that the intrinsic nature of an ideal glass is closely associated with a flat potential landscape. We adopt the $glue$ potential to describe the atomic interaction of Al. This potential can correctly reproduce many basic properties of aluminum in crystalline and non-crystalline phases.[23] The constant-temperature MD method without any boundary conditions is used in the calculations, and any global motion of clusters is carefully eliminated. To obtain a reliable result, the simulation spans the sub-microsecond scale in sub-picosecond steps. To characterize the shape of a cluster, the principal radii of gyration are calculated. In the present calculations, the heat capacity is based on a constant-temperature ensemble, and the volume of clusters is calculated based on the Wigner-Seitz primitive cell approximation.[24] Diffusion constants, which are an important thermodynamic quantity for identifying phases, are obtained by calculating the mean-square displacement of each atom. To characterize a cooperative motion among atoms, we define the time-dependent displacement ($R_c(t)$) as $$ R_c(t)=\Big(\frac{1}{N}\sum_i^N [r_i(t)-r_i(t+\Delta t)]^2\Big)^{1/2}, $$ with $\Delta t=5$ ps. Here we also provide the direct potential landscape from an SSW calculation. For each cluster, we perform 10 parallel SSW runs and collected 105 minima. To identify cluster structures, a distance-weighted Steinhardt-type order parameter (OP)[25] is used to distinguish distinct minima. The original Steinhardt (OP) considers only the first shell bonds,[25] To better distinguish structures, here we design a distance-weighted OP,[26] $$ {\rm OP}_l=\Big(\frac{4\pi}{2l+1}\sum_{m=-l}^{l}|\frac{1}{N_{\rm bonds}}\sum_{i\neq j}e^{-\frac{r_{ij}-r_c}{2r_c}}Y_{lm}({\boldsymbol n})|^2\Big)^{1/2}, $$ where $Y_{lm}$ is the spherical harmonic function of degree $l$ and order $m$; ${\boldsymbol n}$ is the normalized direction between all bonded atoms; $r_{ij}$ is the distance between the atom $i$ and $j$; $r_c$ is set as 60% of the typical single bond length for $i$th and $j$th atom; and $N_{\rm bonds}$ is the number of bonds (in the first bonding shell). By choosing a suitable degree $l$, the OP can measure the short- and medium-range ordering of atoms in clusters.
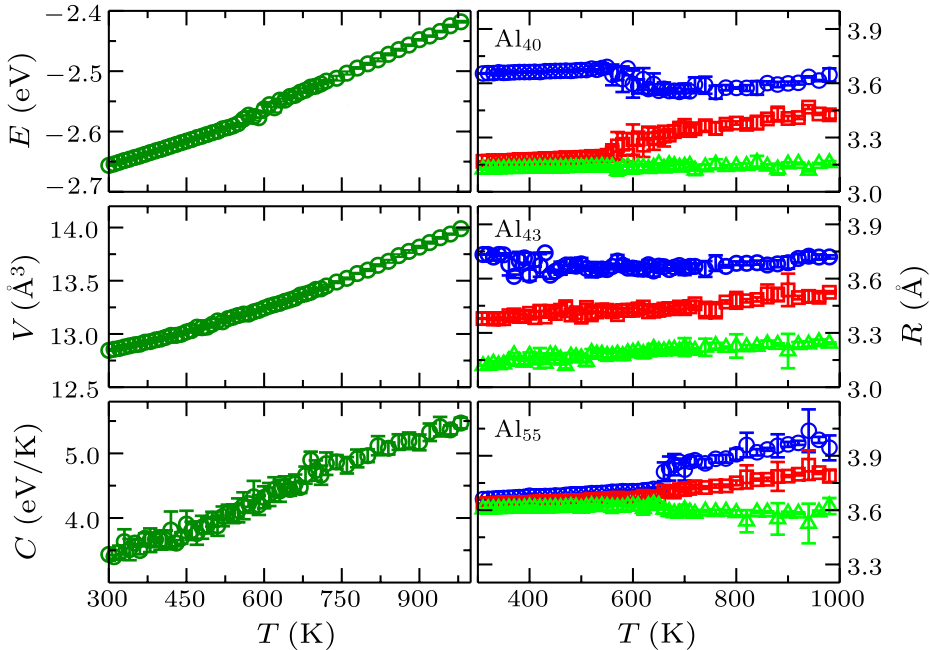
cpl-34-2-026402-fig1.png
Fig. 1. (Color online) Left panel: the energy (upper), volume (middle) and specific heat (lower) as a function of temperature for Al$_{43}$. The continuous change shows a typical glass transition behavior. Right panel: three principal radii of gyration ($R_1,2,3$ indicated by different colors) for Al$_{40}$ (upper), Al$_{43}$ (middle), and Al$_{55}$ (lower). Around $T_{\rm s}$ ($\sim$350 K), the shape of Al$_{43}$ begins to change, while the shape of Al$_{40}$ and Al$_{55}$ is unchanged until melting.
Figure 1 shows the current calculations of the energy, volume and specific heat of Al$_{43}$. One can see that the continuous change in the energy (upper panel), volume (middle panel), and specific heat (lower panel), indicates typical features of the GT. Similar calculations are also performed on Al$_{55}$ and Al$_{40}$ with the results showing that both exhibit typical first-order transition behavior, in agreement with the previous studies.[15] From Fig. 1, one can see that around 350 K, referred to as the starting temperature of the GT ($T_{\rm s}$) (see below), the specific heat has a small jump. Meanwhile the shape of clusters begins to change, as indicated by the principal radii of gyration (right panel of Fig. 1). Since the system is in a well-defined liquid state above 550 K (see below), the GT range can be defined from 350 K to 550 K. In the following we focus on this temperature range. We find that, before melting to a normal liquid state, atoms in the GS display a remarkable cooperative diffusion, which is intrinsically different from that exhibited by liquid states. Figure 2 depicts the diffusion constants versus temperature for the three clusters. It can be seen that above 550 K the diffusion constants show a clear Arrhenius temperature dependence, and all three clusters are in the same liquid states with the same diffusion constants. At low temperatures, before melting, no diffusion has been detected for Al$_{55}$ and Al$_{40}$. However, we clearly identify an Arrhenius temperature dependence for diffusion in the GS for Al$_{43}$ as shown in Fig. 2 (see the black dashed line). This is quite surprising, since for the conventional GS or supercooled liquids, diffusive behavior is usually believed to have a non-Arrhenius character.[5,27] More surprising, contrary to the intuitive picture, the activation energy in the GS is even smaller than that in the liquid state. This shows that the GS and the liquid state are different states. This is strong evidence that the GS is not a supercooled liquid state.
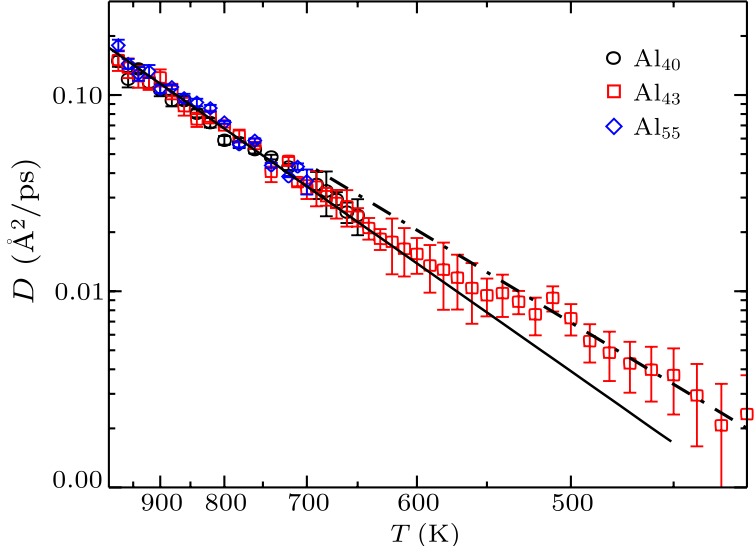
cpl-34-2-026402-fig2.png
Fig. 2. (Color online) Diffusion constants versus temperature for Al$_{40}$, Al$_{43}$ and Al$_{55}$, where the $y$-axis is logarithmic and the $x$-axis is reciprocal temperature. The dashed and solid lines are the Arrhenius fits to the data. The difference in slope of the fitted lines indicates different activation energies.
All the atoms contribute to the diffusion in the GT range, not only surface atoms. To illustrate this point, we calculate the diffusion constant of each atom versus its average position, which is shown in the lower panel of Fig. 3. At 600 K, the cluster is in a well-defined liquid state. As is expected, the diffusion constant is independent of the atomic position. While at 460 K, even inner atoms in the cluster have significant diffusion, similar to the surface atoms. At this temperature the cluster is still in a solid state, and the solid-solid structural transition is a straightforward explanation of the atomic diffusions. To further confirm the solid-solid phase transition in the range of the GT, we calculate $R_c(t)$ at three different temperatures as shown in the upper panel of Fig. 3. At 200 K, Al$_{43}$ is obviously in a well-defined solid state, the atoms vibrate around their equilibrium positions, and no diffusion occurs. In this case, $R_c(t)$ has a very small amplitude, and a small variation with time. At 600 K in the liquid state, although $R_c(t)$ is large, it is consistent with time. This is typical behavior for atomic diffusion of liquids due to less cooperation among atoms. On the other hand, at 460 K in the GS, $R_c(t)$ shows a remarkable variation with time, with some periods essentially as for 200 K and others consistent with 600 K. This indicates that atom diffusion is induced by a cooperative motion in a short time, i.e., a solid-solid transition. It should be noted that the cooperative motion in the ideal GS is different from that reported in supercooled molecular liquids, which display a non-Arrhenius character.[5,27]
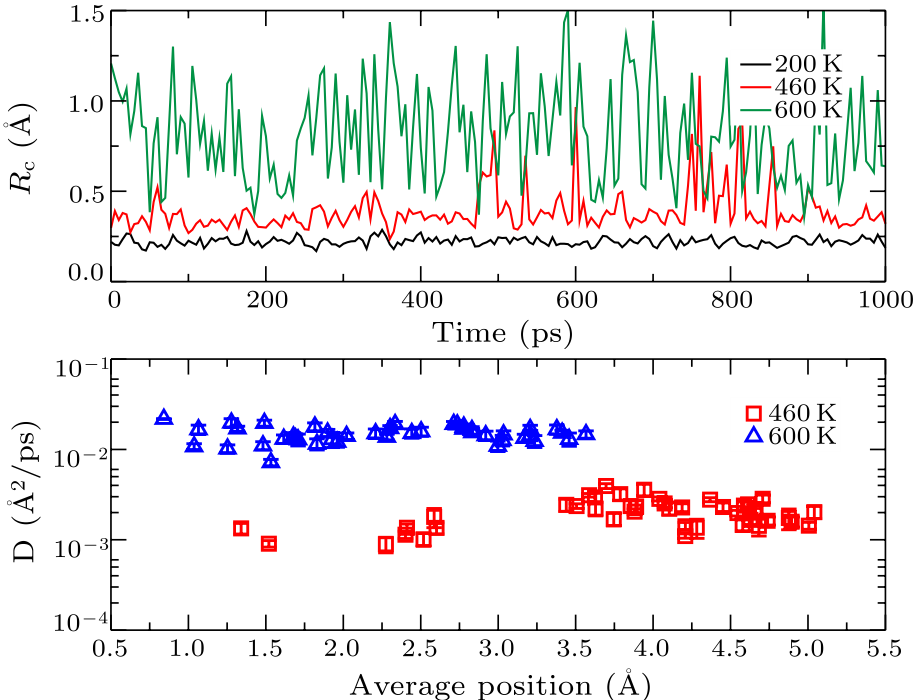
cpl-34-2-026402-fig3.png
Fig. 3. (Color online) Upper panel: the time-dependent displacement for three temperatures. At 460 K, although the displacement is notable, it only occurs in several short durations, which indicates a cooperative motion of atoms in the glass transition range. Lower panel: the diffusion constant of each atom versus its average position. In the glass transition range, the inner atoms have non-negligible diffusion.
The above results suggest that the GT being associated with solid-solid structure transitions implies that the GS must be in a region with flat potential landscape. The phase diagrams for Al$_{43}$ and Al$_{55}$ based on those minima are shown in the upper panel of Fig. 4. Possible phase transformation paths are shown in the lower panel of Fig. 4, where each step has the lowest barrier to the most accessible metastable configuration from the current local minima. As is expected, the symmetric cluster (Al$_{55}$) has high stability, reflected in a larger energy difference (0.4 eV) between the ground state and the second most stable state, as well as a large energy barrier of about 0.75 eV from the ground state to the most accessible metastable state. On the contrary, for the ideal glass Al$_{43}$, the energy difference between the ground state and the second most stable state is very small, only 0.06 eV. The energy barrier from the ground state to the most accessible metastable state is also small, only 0.27 eV. This energy barrier should be responsible for the onset of the GS, namely $T_{\rm s}$. Once the cluster escapes from the ground state, the energy barriers among different states become much smaller (in the order of 0.1 eV), and the GT begins. Here $T_{\rm s}$ can be considered as the Kauzmann temperature ($T_{\rm K}$),[9] below which the configurational entropy of an ideal glass becomes zero.
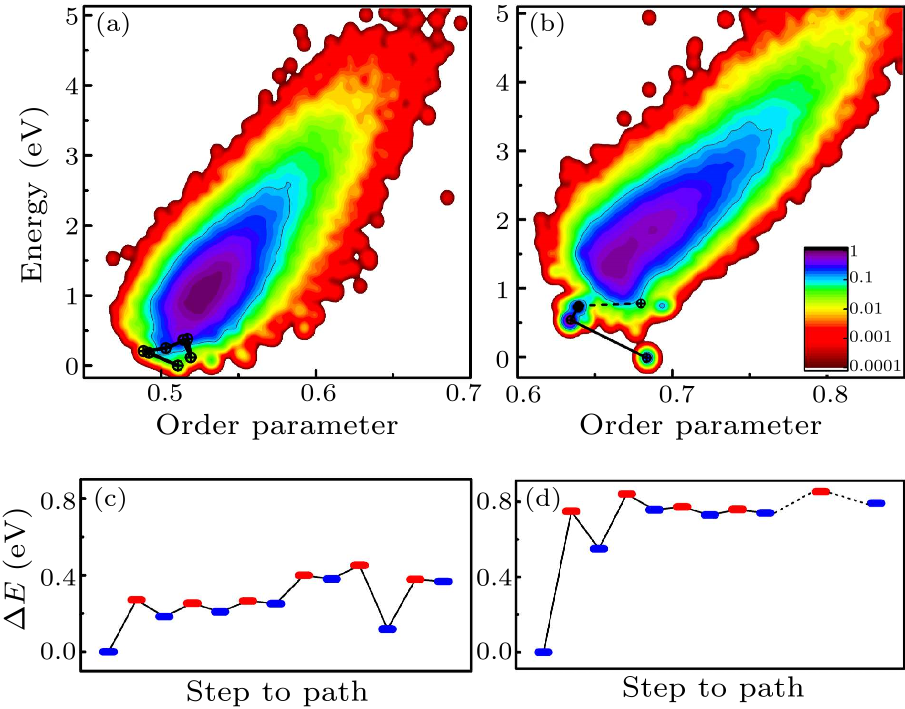
cpl-34-2-026402-fig4.png
Fig. 4. (Color online) Upper panel: the phase diagram of Al$_{43}$ (left) and Al$_{55}$ (right), where the $x$ axis corresponds to the Steinhardt-type order parameter and the $y$ axis corresponds to the potential energy. The colors correspond to the visiting probability of minima during the SSW searches, with the highest probability after gauss broadening being scaled to 1. The black line shows the minima along a possible path for configuration changing from the ground state. Lower panel: the energy profile of the path indicated in upper panel (the black line). The blue bars correspond to the minima, while the orange bars correspond to the transition states. The energy of the global minimum is set to zero in both upper and lower panels.
From the above results and discussions, we are in a position to present a general thermodynamic picture for ideal glasses, as schematically plotted in Fig. 5. A structural phase transition driven by temperature usually involves an entropy increase in the high-temperature phase. As previously suggested,[28] we neglect the difference of vibrational entropies in solid and liquid states, we focus only on the configurational entropy. Below $T_{\rm s}$ ($T_{\rm K}$), since ideal GS has zero configurational entropy, it should behave as a conventional solid (red-dot-dash line in Fig. 5). However above $T_{\rm s}$ the configurational entropy begins to emerge, and the free energy of an ideal glass becomes lower (blue solid line in Fig. 5). With the increasing temperature, the ideal glass can visit more and more configurations, consequently the configurational entropy keeps increasing until the melting temperature ($T_{\rm m}$ in Fig. 5) is reached. Here the free energy curves show a crossover between the ideal GS and liquid state, because the ideal glass is a distinct state rather than a frozen-in supercooled liquid. On the contrary, for GS with a frozen-in supercooled liquid,[3,29,30] the free energy curves will merge into that of liquid state near $T_{\rm m}$, rather than a crossover.
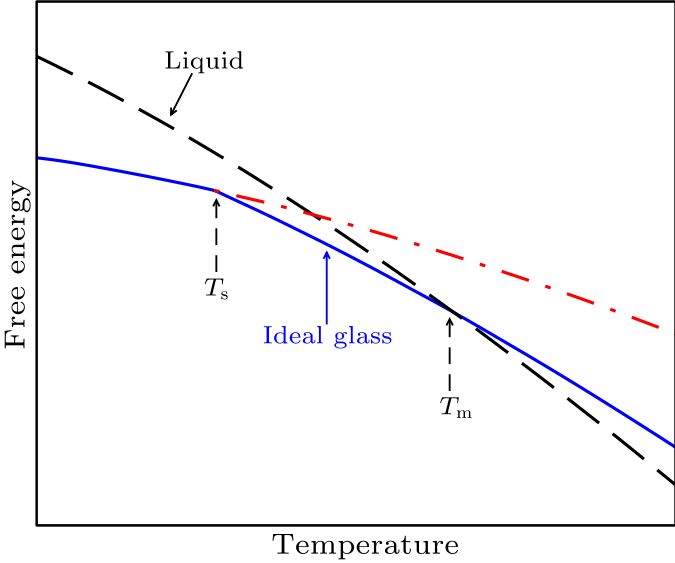
cpl-34-2-026402-fig5.png
Fig. 5. (Color online) The schematic phase diagram for an ideal glass (blue solid line) and a liquid (black dashed line). $T_{\rm m}$ indicates the temperature at which the free energies of the liquid and ideal glass states are equal. $T_{\rm s}$ refers to the emergence of configuration entropies at this temperature. Without these configuration entropies, the free energy of an ideal glass should go along the red dot-dashed line for $T>T_{\rm s}$.
In summary, we have demonstrated that an ideal glass state is a distinct state rather than a frozen-in supercooled liquid. The intrinsic feature of an ideal glass is a flat potential landscape. The glass transition of an ideal glass can be viewed as the process of gaining more and more configurational entropy. Thus, we provide a realistic criterion to define the glass by identifying the special potential landscape not by the structural details. The computation is performed in the Supercomputer of East China Normal University. References What Don't We Know?Formation of Glasses from Liquids and BiopolymersSupercooled liquids and the glass transitionTheoretical perspective on the glass transition and amorphous materialsColloquium : The glass transition and elastic models of glass-forming liquidsSupercooled liquids for pedestriansThe elastic properties, elastic models and elastic perspectives of metallic glassesRelaxation and physical aging in network glasses: a reviewThe Nature of the Glassy State and the Behavior of Liquids at Low Temperatures.Nature of the Glass Transition and the Glassy StateMolecular Transport in Liquids and GlassesOxide Glasses in Light of the “Ideal Glass” Concept: II, Interpretations by Reference to Simeple Ionic Glass BehaviorScaling concepts for the dynamics of viscous liquids near an ideal glassy stateIdeal glass transitions by random pinningStructural properties and glass transition in Al n clustersTheoretical study of the melting of aluminum clustersIon calorimetry: Using mass spectrometry to measure melting pointsStochastic Surface Walking Method for Structure Prediction and Pathway SearchingFrom Atoms to Fullerene: Stochastic Surface Walking Solution for Automated Structure Prediction of Complex MaterialA model metal potential exhibiting polytetrahedral clustersSearching for new TiO 2 crystal phases with better photoactivityConfined platinum nanoparticle in carbon nanotube: structure and oxidationInteratomic Potentials from First-Principles Calculations: The Force-Matching MethodA new constant-pressure molecular dynamics method for finite systemsBond-orientational order in liquids and glassesPressure-induced Silica Quartz Amorphization Studied by Iterative Stochastic Surface Walking Reaction SamplingOn the Temperature Dependence of Cooperative Relaxation Properties in Glass‐Forming LiquidsVibrational and configurational parts of the specific heat at glass formationViscous Liquids and the Glass Transition: A Potential Energy Barrier PictureGeometric Approach to the Dynamic Glass Transition
[1] Kennedy D and Norman C 2005 Science 309 75
[2] Angell C A 1995 Science 267 1924
[3] Debenedetti P G and Stillinger F H 2001 Nature 410 259
[4] Berthier L and Biroli G 2011 Rev. Mod. Phys. 83 587
[5] Dyre J C 2006 Rev. Mod. Phys. 78 953
[6] Cavagna A 2009 Phys. Rep. 476 51
[7] Wang W H 2012 Prog. Mater. Sci. 57 487
[8] Micoulaut M 2016 Rep. Prog. Phys. 79 066504
[9] Kauzmann W 1948 Chem. Rev. 43 219
[10] Gibbs J H and DiMarzio E A 1958 J. Chem. Phys. 28 373
[11] Cohen M H and Turnbull D 1959 J. Chem. Phys. 31 1164
[12] Angell C A 1968 J. Am. Ceram. Soc. 51 125
[13] Kirkpatrick T R, Thirumalai D and Wolynes P G 1989 Phys. Rev. A 40 1045
[14] Cammarota C and Biroli G 2012 Proc. Natl. Acad. Sci. USA 109 8850
[15] Sun D Y and Gong X G 1998 Phys. Rev. B 57 4730
[16] Noya E G, Doye J P K and Calvo F 2006 Phys. Rev. B 73 125407
[17] Neal C M, Starace A K and Jarrold M F 2007 J. Am. Soc. Mass Spectr. 18 74
[18] Shang C and Liu Z P 2013 J. Chem. Theory Comput. 9 1838
[19] Zhang X J, Shang C and Liu Z P 2013 J. Chem. Theory Comput. 9 3252
[20] Doye J P K 2003 J. Chem. Phys. 119 1136
[21] Shang C, Zhao W N and Liu Z P 2015 J. Phys.: Condens. Matter 27 134203
[22] Wei G F, Shang C and Liu Z P 2015 Phys. Chem. Chem. Phys. 17 2078
[23] Ercolessi F and Adams J B 1994 Europhys. Lett. 26 583
[24] Sun D Y and Gong X G 2002 J. Phys.: Condens. Matter 14 L487
[25] Steinhardt P J, Nelson D R and Ronchetti M 1983 Phys. Rev. B 28 784
[26] Zhang X J, Shang C and Liu Z P 2017 Phys. Chem. Chem. Phys. (accepted)
[27] Adam G and Gibbs J H 1965 J. Chem. Phys. 43 139
[28] Tombari E, Ferrari C, Salvetti G and Johari G P 2008 Phys. Rev. B 77 024304
[29] Goldstein M 1969 J. Chem. Phys. 51 3728
[30] Grigera T S, Cavagna A, Giardina I and Parisi G 2002 Phys. Rev. Lett. 88 055502