| GENERAL |
 |
|

|
|
|
Topological Plasma Transport from a Diffusion View |
| Zhoufei Liu and Jiping Huang* |
| Department of Physics, State Key Laboratory of Surface Physics, and Key Laboratory of Micro and Nano Photonic Structures (MOE), Fudan University, Shanghai 200438, China |
|
| Cite this article: |
|
Zhoufei Liu and Jiping Huang 2023 Chin. Phys. Lett. 40 110305 |
|
|
|
|
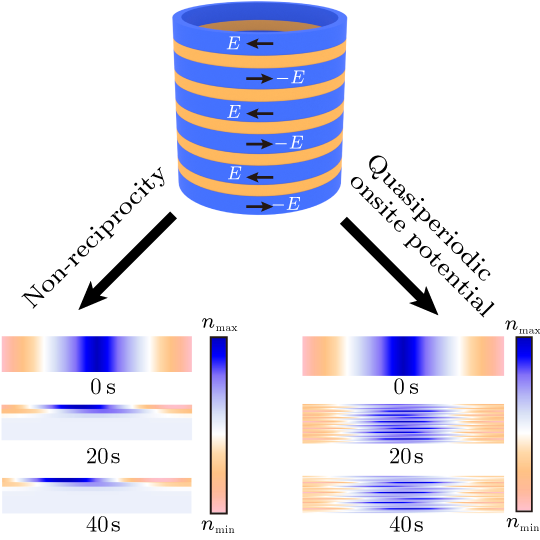
Abstract Recent studies have identified plasma as a topological material. Yet, these researches often depict plasma as a fluid governed by electromagnetic fields, i.e., a classical wave system. Indeed, plasma transport can be characterized by a unique diffusion process distinguished by its collective behaviors. We adopt a simplified diffusion-migration method to elucidate the topological plasma transport. Drawing parallels to the thermal conduction-convection system, we introduce a double-ring model to investigate the plasma density behaviors in the anti-parity-time reversal (APT) unbroken and broken phases. Subsequently, by augmenting the number of rings, we have established a coupled ring chain structure. This structure serves as a medium for realizing the APT symmetric one-dimensional (1D) reciprocal model, representing the simplest tight-binding model with a trivial topology. To develop a model featuring topological properties, we should modify the APT symmetric 1D reciprocal model from the following two aspects: hopping amplitude and onsite potential. From the hopping amplitude, we incorporate the non-reciprocity to facilitate the non-Hermitian skin effect, an intrinsic non-Hermitian topology. Meanwhile, from the onsite potential, the quasiperiodic modulation has been adopted onto the APT symmetric 1D reciprocal model. This APT symmetric 1D Aubry–André–Harper model is of topological nature. Additionally, we suggest the potential applications for these diffusive plasma topological states. This study establishes a diffusion-based approach to realize topological states in plasma, potentially inspiring further advancements in plasma physics.
|
|
Received: 07 October 2023
Express Letter
Published: 31 October 2023
|
|
|
|
|
|
|
|
| [1] | Lieberman M A and Lichtenberg A J 2005 Principles of Plasma Discharges and Materials Processing (New Jersey: Wiley Interscience) |
| [2] | Chen F F 1974 Introduction to Plasma Physics and Controlled Fusion (Switzerland: Springer) |
| [3] | Zheng B C, Fu Y Y, Wang K L, Schuelke T, and Fan Q H 2021 Plasma Sources Sci. Technol. 30 035019 |
| [4] | Huang C W, Chen Y C, and Nishimura Y 2015 IEEE Trans. Plasma Sci. 43 675 |
| [5] | Cui S H, Wu Z Z, Lin H, Xiao S, Zheng B C, Liu L L, An X K, Fu R K Y, Tian X B, Tan W C, and Chu P K 2019 J. Appl. Phys. 125 063302 |
| [6] | Zhang Z R and Huang J P 2022 Chin. Phys. Lett. 39 075201 |
| [7] | Zhang Z R, Xu L J, Qu T, Lei M, Lin Z K, Ouyang X P, Jiang J H, and Huang J P 2023 Nat. Rev. Phys. 5 218 |
| [8] | Yang F B, Zhang Z R, Xu L J, Liu Z F, Jin P, Zhuang P F, Lei M, Liu J R, Jiang J H, Ouyang X P, Marchesoni F, and Huang J P 2023 Rev. Mod. Phys. (in press) |
| [9] | Hasan M Z and Kane C L 2010 Rev. Mod. Phys. 82 3045 |
| [10] | Qi X L and Zhang S C 2011 Rev. Mod. Phys. 83 1057 |
| [11] | Kane C L and Mele E J 2005 Phys. Rev. Lett. 95 226801 |
| [12] | König M, Wiedmann S, Brune C, Roth A, Buhmann H, Molenkamp L W, Qi X L, and Zhang S C 2007 Science 318 766 |
| [13] | Armitage N P, Mele E J, and Vishwanath A 2018 Rev. Mod. Phys. 90 015001 |
| [14] | Lu L, Joannopoulos J D, and Soljačić M 2014 Nat. Photonics 8 821 |
| [15] | Ozawa T, Price H M, Amo A, Goldman N, Hafezi M, Lu L, Rechtsman M C, Schuster D, Simon J, Zilberberg O, and Carusotto I 2019 Rev. Mod. Phys. 91 015006 |
| [16] | Cao J H, Kavokin A V, and Nalitov A V 2022 Prog. Electromagn. Res. 173 141 |
| [17] | Xue H R, Yang Y H, and Zhang B L 2022 Nat. Rev. Mater. 7 974 |
| [18] | Tsang L, Liao T H, and Tan S R 2021 Prog. Electromagn. Res. 171 137 |
| [19] | Jia D, Wang Y, Ge Y, Yuan S Q, and Sun H X 2021 Prog. Electromagn. Res. 172 13 |
| [20] | Zhang C X, Li T J, Xu L J, and Huang J P 2023 Chin. Phys. Lett. 40 054401 |
| [21] | Yin H Y and Fan C Z 2023 Chin. Phys. Lett. 40 077801 |
| [22] | He Z G, Yuan K, Xiong G H, and Wang J 2023 Chin. Phys. Lett. 40 104402 |
| [23] | Wang Y, Han T C, Liang D F, and Deng L J 2023 Chin. Phys. Lett. 40 104101 |
| [24] | Lou Q and Xia M G 2023 Chin. Phys. Lett. 40 094401 |
| [25] | Li Y and Li J X 2021 Chin. Phys. Lett. 38 030501 |
| [26] | Ju R, Xu G Q, Xu L J, Qi M H, Wang D, Cao P C, Xi R, Shou Y F, Chen H S, Qiu C W, and Li Y 2023 Adv. Mater. 35 2209123 |
| [27] | Liu Z F, Xu L J, and Huang J P 2022 arXiv:2206.09837 [physics.app-ph] |
| [28] | Liu Z F 2023 arXiv:2309.09681 [physics.app-ph] |
| [29] | Xu G Q, Li Y, Li W, Fan S H, and Qiu C W 2021 Phys. Rev. Lett. 127 105901 |
| [30] | Xu G Q, Yang Y H, Zhou X, Chen H S, Alù A, and Qiu C W 2022 Nat. Phys. 18 450 |
| [31] | Xu G Q, Zhou X, Yang S H, Wu J, and Qiu C W 2023 Nat. Commun. 14 3252 |
| [32] | Xu L J and Huang J P 2021 Europhys. Lett. 134 60001 |
| [33] | Xu L J, Wang J, Dai G L, Yang S, Yang F B, Wang G, and Huang J P 2021 Int. J. Heat Mass Transfer 165 120659 |
| [34] | Parker J B, Burby J W, Marston J B, and Tobias S M 2020 Phys. Rev. Res. 2 033425 |
| [35] | Parker J B, Burby J W, Marston J B, Tobias S M, and Zhu Z Y 2020 Phys. Rev. Lett. 124 195001 |
| [36] | Fu Y C and Qin H 2021 Nat. Commun. 12 3924 |
| [37] | Gao W L, Yang B, Lawrence M, Fang F Z, Beri B, and Zhang S 2016 Nat. Commun. 7 12435 |
| [38] | Li Y, Peng Y G, Han L, Miri M A, Li W, Xiao M, Zhu X F, Zhao J L, Alù A, Fan S H, and Qiu C W 2019 Science 364 170 |
| [39] | Li Z P, Cao G T, Li C H, Dong S H, Deng Y, Liu X K, Ho J S, and Qiu C W 2021 Prog. Electromagn. Res. 171 1 |
| [40] | Cao P C, Li Y, Peng Y G, Qi M H, Huang W X, Li P Q, and Zhu X F 2021 Commun. Phys. 4 230 |
| [41] | Huang Q K L, Liu Y K, Cao P C, Zhu X F, and Li Y 2023 Chin. Phys. Lett. 40 106601 |
| [42] | Hu B L, Zhang Z W, Yue Z C, Liao D W, Liu Y M, Zhang H X, Cheng Y, Liu X J, and Christensen J 2023 Phys. Rev. Lett. 131 066601 |
| [43] | Yao S Y and Wang Z 2018 Phys. Rev. Lett. 121 086803 |
| [44] | Okuma N, Kawabata K, Shiozaki K, and Sato M 2020 Phys. Rev. Lett. 124 086801 |
| [45] | Yan Q H, Chen H S, and Yang Y H 2021 Prog. Electromagn. Res. 172 33 |
| [46] | Hatano N and Nelson D R 1996 Phys. Rev. Lett. 77 570 |
| [47] | Cao P C, Peng Y G, Li Y, and Zhu X F 2022 Chin. Phys. Lett. 39 057801 |
| [48] | Aubry S and André G 1980 Ann. Isr. Phys. Soc. 3 133 |
| [49] | Harper P G 1955 Proc. Phys. Soc. Sect. A 68 874 |
| [50] | Liu Z F and Huang J P 2022 arXiv:2208.06765 [physics.app-ph] |
| [51] | Longhi S 2019 Phys. Rev. Lett. 122 237601 |
| [52] | Longhi S 2019 Phys. Rev. B 100 125157 |
| [53] | Budich J C and Bergholtz E J 2020 Phys. Rev. Lett. 125 180403 |
| [54] | Jin P, Xu L J, Xu G Q, Li J X, Qiu C W, and Huang J P 2023 Adv. Mater. (in press) |
|
|
Viewed |
|
|
|
Full text
|
|
|
|
|
Abstract
|
|
|
|
|