| GENERAL |
 |
|

|
|
|
A Lattice Non-Perturbative Definition of an SO(10) Chiral Gauge Theory and Its Induced Standard Model |
| WEN Xiao-Gang |
1Perimeter Institute for Theoretical Physics, Waterloo, Ontario N2L 2Y5, Canada
2Department of Physics, Massachusetts Institute of Technology, Cambridge, Massachusetts 02139, USA |
|
| Cite this article: |
|
WEN Xiao-Gang 2013 Chin. Phys. Lett. 30 111101 |
|
|
|
|
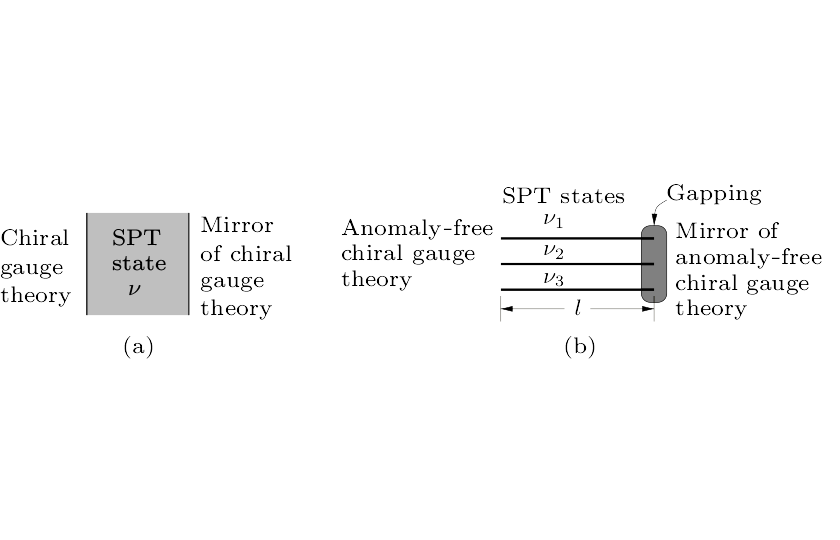
Abstract The standard model is a chiral gauge theory where the gauge fields couple to the right-hand and the left-hand fermions differently. The standard model is defined perturbatively and describes all elementary particles (except gravitons) very well. However, for a long time, we do not know if we can have a non-perturbative definition of the standard model as a Hamiltonian quantum mechanical theory. Here we propose a way to give a modified standard model (with 48 two-component Weyl fermions) a non-perturbative definition by embedding the modified standard model into an SO(10) chiral gauge theory. We show that the SO(10) chiral gauge theory can be put on a lattice (a 3D spatial lattice with a continuous time) if we allow fermions to interact. Such a non-perturbatively defined standard model is a Hamiltonian quantum theory with a finite-dimensional Hilbert space for a finite space volume. More generally, using the defining connection between gauge anomalies and the symmetry-protected topological orders, one can show that any truly anomaly-free chiral gauge theory can be non-perturbatively defined by putting it on a lattice in the same dimension.
|
|
Received: 27 October 2013
Published: 30 November 2013
|
|
| PACS: |
11.15.Ha
|
(Lattice gauge theory)
|
| |
12.39.Fe
|
(Chiral Lagrangians)
|
| |
12.10.Dm
|
(Unified theories and models of strong and electroweak interactions)
|
|
|
|
|
|
[1] Glashow S L 1961 Nucl. Phys. 22 579
[2] Weinberg S 1967 Phys. Rev. Lett. 19 1264
[3] Salam A and Ward J C 1964 Phys. Lett. 13 168
[4] Gell-Mann M 1962 Phys. Rev. 125 1067
[5] Zweig G, Lichtenberg D B (ed) and Rosen S P (ed) 1964 Developments in the Quark Theory of Hadrons vol 1 p 24
[6] Fritzsch H and Gell-Mann M 1972 Proceedings of the XVI International Conference on High Energy Physics ed Jackson J D and Roberts A (Chicago) vol 2 p 135
[7] Kogut J B 1979 Rev. Mod. Phys. 51 659
[8] Kaplan D B 1992 Phys. Lett. B 288 342
[9] Shamir Y 1993 Nucl. Phys. B 406 90
[10] Narayanan R and Neuberger H 1993 Phys. Lett. B 302 62
[11] Narayanan R and Neuberger H 1994 Nucl. Phys. B 412 574
[12] Lüscher M 1999 Nucl. Phys. B 549 295
[13] Neuberger H 2000 Phys. Rev. D 63 014503
[14] Suzuki H 1999 Prog. Theor. Phys. 101 1147
[15] Lüscher M 2001 arXiv:hep-th/0102028
[16] Eichten E and Preskill J 1986 Nucl. Phys. B 268 179
[17] Montvay I 1992 Nucl. Phys. B-Proc. Suppl. 29 159
[18] Bhattacharya T, Martin M R and Poppitz E 2006 Phys. Rev. D 74 085028
[19] Giedt J and Poppitz E 2007 J. High Energy Phys. 1007 076
[20] Smit J 1986 Acta Phys. Pol. B 17 531
[21] Swift P D V 1984 Phys. Lett. B 145 256
[22] Golterman M, Petcher D and Rivas E 1993 Nucl. Phys. B 395 596
[23] Lin L 1994 Phys. Lett. B 324 418
[24] Chen C, Giedt J and Poppitz E 2013 J. High Energy Phys. 1304 131
[25] Banks T and Dabholkar A 1992 Phys. Rev. D 46 4016
[26] Wen X G 2013 Phys. Rev. D 88 045013
[27] Wang J and Wen X G 2013 arXiv:1307.7480 [hep-lat]
[28] Adler S 1969 Phys. Rev. D 177 2426
[29] Bell J and Jackiw R 1969 Nuovo Cimento A 60 47
[30] Wen X G 2013 arXiv:1301.7675 [cond-mat.str-el]
[31] Fritzsch H and Minkowski P 1975 Ann. Phys. 93 193
[32] Georgi H and Glashow S L 1974 Phys. Rev. Lett. 32 438
[33] Gu Z C and Wen X G 2009 Phys. Rev. B 80 155131
[34] Pollmann F, Berg E, Turner A M and Oshikawa M 2009 arXiv:0909.4059 [cond-mat.str-el]
[35] Chen X, Gu Z C and Wen X G 2010 Phys. Rev. B 82 155138
[36] Chen X, Liu Z X and Wen X G 2011 Phys. Rev. B 84 235141
[37] Chen X, Gu Z C, Liu Z X and Wen X G 2013 Phys. Rev. B 87 155114
[38] Chen X, Gu Z C, Liu Z X and Wen X G 2012 Science 338 1604
[39] Lu Y M and Vishwanath A 2012 Phys. Rev. B 86 125119
[40] Liu Z X and Wen X G 2013 Phys. Rev. Lett. 110 067205
[41] Chen X and Wen X G 2012 Phys. Rev. B 86 235135
[42] Senthil T and Levin M 2013 Phys. Rev. Lett. 110 046801
[43] Witten E 1982 Phys. Lett. B 117 324
[44] Gu Z C and Wen X G 2012 arXiv:1201.2648 [cond-mat.str-el]
[45] Creutz M and Horvath I 1994 Phys. Rev. D 50 2297
[46] Qi X L, Hughes T and Zhang S C 2008 Phys. Rev. B 78 195424
[47] Zee A 2003 Quantum Field Theory in a Nutshell (Princeton: Princeton University)
[48] Wess J and Zumino B 1971 Phys. Lett. B 37 95
[49] Witten E 1983 Nucl. Phys. B 223 422 27 October 2013 |
|
Viewed |
|
|
|
Full text
|
|
|
|
|
Abstract
|
|
|
|
|