| GENERAL |
|

|
|
|
Deep Learning Quantum States for Hamiltonian Estimation |
| Xinran Ma1, Z. C. Tu1, and Shi-Ju Ran2* |
1Department of Physics, Beijing Normal University, Beijing 100875, China
2Department of Physics, Capital Normal University, Beijing 100048, China
|
|
| Cite this article: |
|
Xinran Ma, Z. C. Tu, and Shi-Ju Ran 2021 Chin. Phys. Lett. 38 110301 |
|
|
|
|
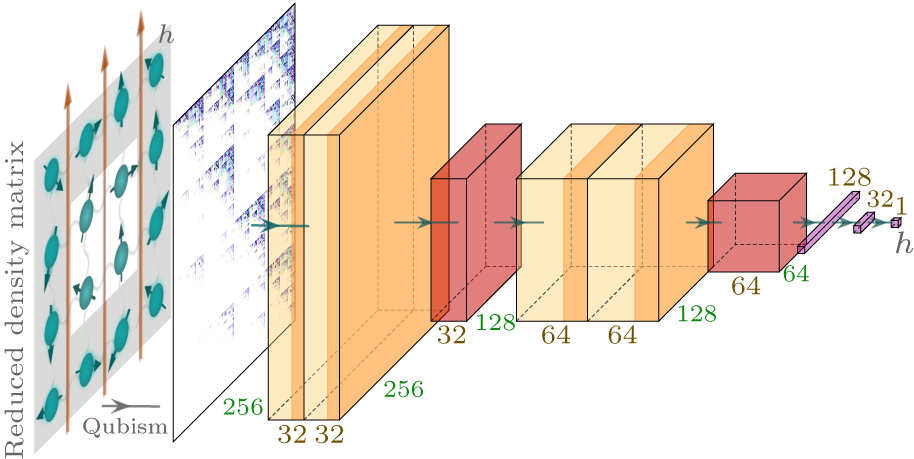
Abstract Human experts cannot efficiently access physical information of a quantum many-body states by simply “reading” its coefficients, but have to reply on the previous knowledge such as order parameters and quantum measurements. We demonstrate that convolutional neural network (CNN) can learn from coefficients of many-body states or reduced density matrices to estimate the physical parameters of the interacting Hamiltonians, such as coupling strengths and magnetic fields, provided the states as the ground states. We propose QubismNet that consists of two main parts: the Qubism map that visualizes the ground states (or the purified reduced density matrices) as images, and a CNN that maps the images to the target physical parameters. By assuming certain constraints on the training set for the sake of balance, QubismNet exhibits impressive powers of learning and generalization on several quantum spin models. While the training samples are restricted to the states from certain ranges of the parameters, QubismNet can accurately estimate the parameters of the states beyond such training regions. For instance, our results show that QubismNet can estimate the magnetic fields near the critical point by learning from the states away from the critical vicinity. Our work provides a data-driven way to infer the Hamiltonians that give the designed ground states, and therefore would benefit the existing and future generations of quantum technologies such as Hamiltonian-based quantum simulations and state tomography.
|
|
Received: 15 August 2021
Express Letter
Published: 11 October 2021
|
|
| PACS: |
03.67.Ac
|
(Quantum algorithms, protocols, and simulations)
|
| |
02.30.Zz
|
(Inverse problems)
|
| |
03.65.Wj
|
(State reconstruction, quantum tomography)
|
| |
03.67.Lx
|
(Quantum computation architectures and implementations)
|
| |
07.05.Mh
|
(Neural networks, fuzzy logic, artificial intelligence)
|
| |
75.10.Jm
|
(Quantized spin models, including quantum spin frustration)
|
|
|
| Fund: Supported by the National Natural Science Foundation of China (Grant Nos. 12004266, 11834014 and 11975050), the Beijing Natural Science Foundation (Grant Nos. 1192005 and Z180013), the Foundation of Beijing Education Committees (Grant No. KM202010028013), and the Academy for Multidisciplinary Studies, Capital Normal University. |
|
|
|
| [1] | Verstraete F, Murg V, and Cirac J I 2008 Adv. Phys. 57 143 |
| [2] | Orús R 2019 Nat. Rev. Phys. 1 538 |
| [3] | Ran S J, Tirrito E, Peng C, Chen X, Tagliacozzo L, Su G, and Lewenstein M 2020 Tensor Network Contractions: Methods and Applications to Quantum Many-Body Systems Part of the Lecture Notes in Physics book series (LNP, volume 964) (Berlin: Springer) |
| [4] | Ceperley D and Alder B 1986 Science 231 555 |
| [5] | Nightingale M P and Umrigar C J 1998 Quantum Monte Carlo Methods in Physics and Chemistry (Berlin: Springer) |
| [6] | Wang L 2016 Phys. Rev. B 94 195105 |
| [7] | Carrasquilla J and Melko R G 2017 Nat. Phys. 13 431 |
| [8] | Van Nieuwenburg E P, Liu Y H, and Huber S D 2017 Nat. Phys. 13 435 |
| [9] | Zhang P, Shen H, and Zhai H 2018 Phys. Rev. Lett. 120 066401 |
| [10] | Rem B S, Käming N, Tarnowski M, Asteria L, Fläschner N, Becker C, Sengstock K, and Weitenberg C 2019 Nat. Phys. 15 917 |
| [11] | Rodriguez-Nieva J F and Scheurer M S 2019 Nat. Phys. 15 790 |
| [12] | Scheurer M S and Slager R J 2020 Phys. Rev. Lett. 124 226401 |
| [13] | Rupp M, Tkatchenko A, Müller K R, and Von Lilienfeld O A 2012 Phys. Rev. Lett. 108 058301 |
| [14] | Xie T and Grossman J C 2018 Phys. Rev. Lett. 120 145301 |
| [15] | Hanakata P Z, Cubuk E D, Campbell D K, and Park H S 2018 Phys. Rev. Lett. 121 255304 |
| [16] | Carleo G and Troyer M 2017 Science 355 602 |
| [17] | Choo K, Carleo G, Regnault N, and Neupert T 2018 Phys. Rev. Lett. 121 167204 |
| [18] | Glasser I, Pancotti N, August M, Rodriguez I D, and Cirac J I 2018 Phys. Rev. X 8 011006 |
| [19] | Deng D L, Li X, and Sarma S D 2017 Phys. Rev. B 96 195145 |
| [20] | Avella A and Mancini F et al. 2012 Strongly Correlated Systems (Berlin: Springer) |
| [21] | Kuramoto Y 2020 Quantum Many-Body Physics (Berlin: Springer) |
| [22] | Fournier R, Wang L, Yazyev O V, and Wu Q 2020 Phys. Rev. Lett. 124 056401 |
| [23] | Teoh Y H, Drygala M, Melko R G, and Islam R 2020 Quantum Sci. Technol. 5 024001 |
| [24] | Hanakata P Z, Cubuk E D, Campbell D K, and Park H S 2020 Phys. Rev. Res. 2 042006 |
| [25] | Arsenault L F, Neuberg R, Hannah L A, and Millis A J 2017 Inverse Probl. 33 115007 |
| [26] | Xin T, Lu S, Cao N, Anikeeva G, Lu D, Li J, Long G, and Zeng B 2019 npj Quantum Inf. 5 1 |
| [27] | Hegde G and Bowen R C 2017 Sci. Rep. 7 42669 |
| [28] | Li X Y, Lou F, Gong X, and Xiang H 2020 New J. Phys. 22 053036 |
| [29] | Sehanobish A, Corzo H H, Kara O, and van Dijk D 2020 arXiv:2006.13297 [cs.LG] |
| [30] | LeCun Y, Boser B, Denker J S, Henderson D, Howard R E, Hubbard W, and Jackel L D 1989 Neural Comput. 1 541 |
| [31] | Krizhevsky A, Sutskever I, and Hinton G E 2017 Commun. ACM 60 84 |
| [32] | Aloysius N and Geetha M 2017 2017 International Conference on Communication and Signal Processing pp 0588–0592 |
| [33] | Yao G, Lei T, and Zhong J 2019 Pattern Recognit. Lett. 118 14 |
| [34] | Sultana F, Sufian A, and Dutta P 2020 Intelligent Computing: Image Processing Based Applications (Berlin: Springer) p 1 |
| [35] | Berthusen N F, Sizyuk Y, Scheurer M S, and Orth P P 2020 arXiv:2011.12911 [cond-mat.str-el] |
| [36] | Goh G B, Siegel C, Vishnu A, Hodas N O, and Baker N 2017 arXiv:1706.06689 [stat.ML] |
| [37] | Laanait N, Romero J, Yin J, Young M T, Treichler S, Starchenko V, Borisevich A, Sergeev A, and Matheson M 2019 arXiv:1909.11150 [cs.LG] |
| [38] | Das A and Chakrabarti B K 2008 Rev. Mod. Phys. 80 1061 |
| [39] | Rodrı́guez-Laguna J, Migdał P, Berganza M I N, Lewenstein M, and Sierra G 2012 New J. Phys. 14 053028 |
| [40] | White S R 1992 Phys. Rev. Lett. 69 2863 |
| [41] | White S R 1993 Phys. Rev. B 48 10345 |
| [42] | Hinton G, Srivastava N, and Swersky K 2012 Neural Networks for Machine Learning Lecture 6a: Overview of Mini-batch Gradient Descent |
| [43] | Verstraete F and Cirac J I 2006 Phys. Rev. B 73 094423 |
| [44] | Zauner V, Draxler D, Vanderstraeten L, Degroote M, Haegeman J, Rams M M, Stojevic V, Schuch N, and Verstraete F 2015 New J. Phys. 17 053002 |
| [45] | Franchini F 2017 An Introduction to Integrable Techniques for One-dimensional Quantum Systems (Berlin: Springer) |
| [46] | Schaffer R, Huh Y, Hwang K, and Kim Y B 2017 Phys. Rev. B 95 054410 |
| [47] | Repellin C, He Y C, and Pollmann F 2017 Phys. Rev. B 96 205124 |
| [48] | Mitarai K, Negoro M, Kitagawa M, and Fujii K 2018 Phys. Rev. A 98 032309 |
| [49] | Liu J G and Wang L 2018 Phys. Rev. A 98 062324 |
| [50] | Zhu D, Linke N M, Benedetti M, Landsman K A, Nguyen N H, Alderete C H, Perdomo-Ortiz A, Korda N, Garfoot A, Brecque C et al. 2019 Sci. Adv. 5 eaaw9918 |
| [51] | Georgescu I M, Ashhab S, and Nori F 2014 Rev. Mod. Phys. 86 153 |
| [52] | Vogel K and Risken H 1989 Phys. Rev. A 40 2847 |
| [53] | Cramer M, Plenio M B, Flammia S T, Somma R, Gross D, Bartlett S D, Landon-Cardinal O, Poulin D, and Liu Y K 2010 Nat. Commun. 1 149 |
| [54] | Lanyon B, Maier C, Holzäpfel M, Baumgratz T, Hempel C, Jurcevic P, Dhand I, Buyskikh A, Daley A, Cramer M et al. 2017 Nat. Phys. 13 1158 |
| [55] | Cook S A 1971 The Complexity of Theorem-Proving Procedures in STOC'71: Proceedings of the Third Annual Acm Symposium on Theory of Computing (New York: ACM Press) pp 151–158 |
| [56] | Krzakala F and Zdeborová L 2009 Phys. Rev. Lett. 102 238701 |
|
|
Viewed |
|
|
|
Full text
|
|
|
|
|
Abstract
|
|
|
|
|