| CONDENSED MATTER: ELECTRONIC STRUCTURE, ELECTRICAL, MAGNETIC, AND OPTICAL PROPERTIES |
 |
|

|
|
|
Metal to Orthogonal Metal Transition |
| Chuang Chen1, Xiao Yan Xu2,3, Yang Qi4,5,6, Zi Yang Meng7,1,8** |
1Beijing National Laboratory for Condensed Matter Physics and Institute of Physics, Chinese Academy of Sciences, Beijing 100190
2Department of Physics, Hong Kong University of Science and Technology, Clear Water Bay, Hong Kong
3Department of Physics, University of California at San Diego, La Jolla, California 92093, USA
4Center for Field Theory and Particle Physics, Department of Physics, Fudan University, Shanghai 200433
5State Key Laboratory of Surface Physics, Fudan University, Shanghai 200433
6Collaborative Innovation Center of Advanced Microstructures, Nanjing 210093
7Department of Physics and HKU-UCAS Joint Institute of Theoretical and Computational Physics, The University of Hong Kong, Pokfulam Road, Hong Kong
8Songshan Lake Materials Laboratory, Dongguan 523808
|
|
| Cite this article: |
|
Chuang Chen, Xiao Yan Xu, Yang Qi et al 2020 Chin. Phys. Lett. 37 047103 |
|
|
|
|
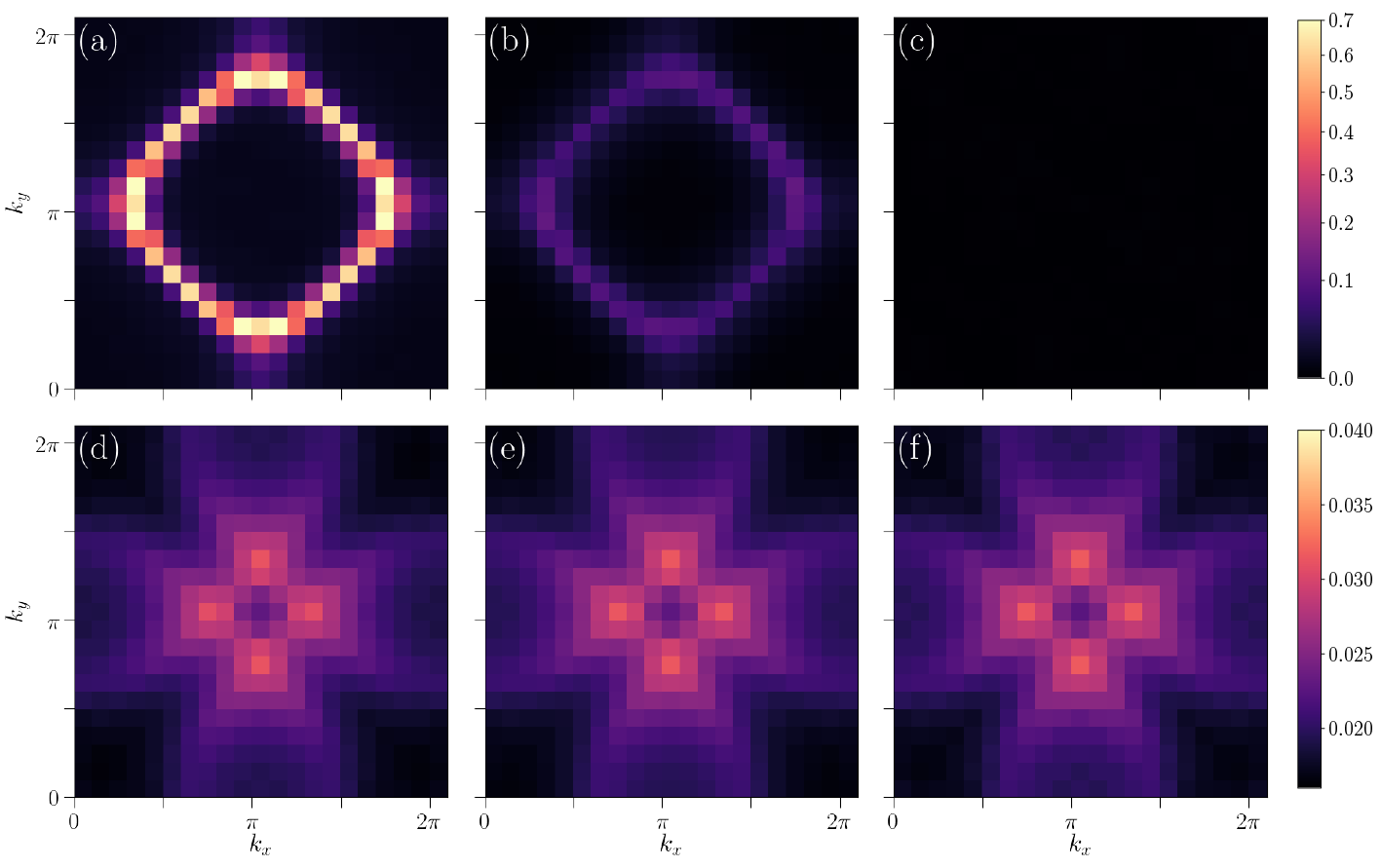
Abstract Orthogonal metal is a new quantum metallic state that conducts electricity but acquires no Fermi surface (FS) or quasiparticles, and hence orthogonal to the established paradigm of Landau's Fermi-liquid (FL). Such a state may hold the key of understanding the perplexing experimental observations of quantum metals that are beyond FL, i.e., dubbed non-Fermi-liquid (nFL), ranging from the Cu- and Fe-based oxides, heavy fermion compounds to the recently discovered twisted graphene heterostructures. However, to fully understand such an exotic state of matter, at least theoretically, one would like to construct a lattice model and to solve it with unbiased quantum many-body machinery. Here we achieve this goal by designing a 2D lattice model comprised of fermionic and bosonic matter fields coupled with dynamic $\mathbb{Z}_2$ gauge fields, and obtain its exact properties with sign-free quantum Monte Carlo simulations. We find that as the bosonic matter fields become disordered, with the help of deconfinement of the $\mathbb{Z}_2$ gauge fields, the system reacts with changing its nature from the conventional normal metal with an FS to an orthogonal metal of nFL without FS and quasiparticles and yet still responds to magnetic probe like an FL. Such a quantum phase transition from a normal metal to an orthogonal metal, with its electronic and magnetic spectral properties revealed, is calling for the establishment of new paradigm of quantum metals and their transition with conventional ones.
|
|
Received: 05 October 2019
Published: 27 March 2020
|
|
| PACS: |
71.10.-w
|
(Theories and models of many-electron systems)
|
| |
71.27.+a
|
(Strongly correlated electron systems; heavy fermions)
|
| |
02.70.Ss
|
(Quantum Monte Carlo methods)
|
|
|
| Fund: Supported by the National Key R&D Program of China (Grant No. 2016YFA0300502), the National Science Foundation of China (Grant Nos. 11574359 and 11674370), the Research Grants Council of Hong Kong SAR China under Grant Nos. 17303019, C6026-16W, 16324216, and 16307117, the National Basic Research Program of China (Grant No. 2015CB921700), and the National Natural Science Foundation of China (Grant No. 11874115). |
|
|
|
| [1] | Luttinger J M 1960 Phys. Rev. 119 1153 | | [2] | Oshikawa M 2000 Phys. Rev. Lett. 84 3370 | | [3] | Paramekanti A and Vishwanath A 2004 Phys. Rev. B 70 245118 | | [4] | Löhneysen H v, Rosch A, Vojta M and Wölfle P 2007 Rev. Mod. Phys. 79 1015 | | [5] | Keimer B, Kivelson S A, Norman M R, Uchida S and Zaanen J 2015 Nature 518 179 | | [6] | Gu Y, Liu Z, Xie T, Zhang W, Gong D, Hu D, Ma X, Li C, Zhao L, Lin L, Xu Z, Tan G, Chen G, Meng Z Y, Yang Y f, Luo H and Li S 2017 Phys. Rev. Lett. 119 157001 | | [7] | Wu W, Cheng J, Matsubayashi K, Kong P, Lin F, Jin C, Wang N, Uwatoko Y and Luo J 2014 Nat. Commun. 5 5508 | | [8] | Cheng J and Luo J 2017 J. Phys.: Condens. Matter 29 383003 | | [9] | Matsuda M, Lin F K, Yu R, Cheng J G, Wu W, Sun J P, Zhang J H, Sun P J, Matsubayashi K, Miyake T, Kato T, Yan J Q, Stone M B, Si Q, Luo J L and Uwatoko Y 2018 Phys. Rev. X 8 031017 | | [10] | Stewart G R 2001 Rev. Mod. Phys. 73 797 | | [11] | Custers J, Gegenwart P, Wilhelm H, Neumaier K, Tokiwa Y, Trovarelli O, Geibel C, Steglich F, Pepin C and Coleman P 2003 Nature 424 524 | | [12] | Si Q and Steglich F 2010 Science 329 1161 | | [13] | Steppke A, Küchler R, Lausberg S, Lengyel E, Steinke L, Borth R, Lühmann T, Krellner C, Nicklas M, Geibel C, Steglich F and Brando M 2013 Science 339 933 | | [14] | Cao Y, Fatemi V, Demir A, Fang S, Tomarken S L, Luo J Y, Sanchez-Yamagishi J D, Watanabe K, Taniguchi T, Kaxiras E, Ashoori R C and Jarillo-Herrero P 2018 Nature 556 80 | | [15] | Cao Y, Fatemi V, Fang S, Watanabe K, Taniguchi T, Kaxiras E and Jarillo-Herrero P 2018 Nature 556 43 | | [16] | Cao Y, Chowdhury D, Rodan-Legrain D, Rubies-Bigordà O, Watanabe K, Taniguchi T, Senthil T and Jarillo-Herrero P 2019 arXiv:1901.03710 | | [17] | Shen C, Li N, Wang S, Zhao Y, Tang J, Liu J, Tian J, Chu Y, Watanabe K, Taniguchi T, Yang R, Meng Z Y, Shi D and Zhang G 2019 arXiv:1903.06952 | | [18] | Senthil T, Sachdev S and Vojta M 2003 Phys. Rev. Lett. 90 216403 | | [19] | Punk M, Allais A and Sachdev S 2015 Proc. Natl. Acad. Sci. USA 112 9552 | | [20] | Feldmeier J, Huber S and Punk M 2018 Phys. Rev. Lett. 120 187001 | | [21] | Maldacena J and Stanford D 2016 Phys. Rev. D 94 106002 | | [22] | Hofmann J S, Assaad F F and Grover T 2019 Phys. Rev. B 100 035118 | | [23] | Pan G, Wang Y and Meng Z Y 2020 arXiv:2001.06586 | | [24] | Nandkishore R, Metlitski M A and Senthil T 2012 Phys. Rev. B 86 045128 | | [25] | Rüegg A, Huber S D and Sigrist M 2010 Phys. Rev. B 81 155118 | | [26] | Gazit S, Assaad F F and Sachdev S 2019 arXiv:1906.11250 | | [27] | Huijse L and Sachdev S 2011 Phys. Rev. D 84 026001 | | [28] | Senthil T and Motrunich O 2002 Phys. Rev. B 66 205104 | | [29] | Kaul R K 2012 Physics 5 82 | | [30] | Kogut J B 1979 Rev. Mod. Phys. 51 659 | | [31] | Fradkin E 2013 Field Theories of Condensed Matter Physics 2nd edn (Cambridge University Press) | | [32] | Xu X Y, Liu Z H, Pan G, Qi Y, Sun K and Meng Z Y 2019 J. Phys.: Condens. Matter 31 463001 | | [33] | Xu X Y, Qi Y, Zhang L, Assaad F F, Xu C and Meng Z Y 2019 Phys. Rev. X 9 021022 | | [34] | Liu Y, Wang W, Sun K and Meng Z Y 2020 Phys. Rev. B 101 064308 | | [35] | Hohenadler M and Assaad F F 2018 Phys. Rev. Lett. 121 086601 | | [36] | Hohenadler M and Assaad F F 2019 Phys. Rev. B 100 125133 | | [37] | Xu X Y, Sun K, Schattner Y, Berg E and Meng Z Y 2017 Phys. Rev. X 7 031058 | | [38] | Liu Z H, Xu X Y, Qi Y, Sun K and Meng Z Y 2018 Phys. Rev. B 98 045116 | | [39] | Liu Z H, Pan G, Xu X Y, Sun K and Meng Z Y 2019 Proc. Natl. Acad. Sci. USA 116 16760 | | [40] | Hirsch J E 1985 Phys. Rev. B 31 4403 | | [41] | He Y Y, Wu H Q, You Y Z, Xu C, Meng Z Y and Lu Z Y 2016 Phys. Rev. B 93 115150 | | [42] | Xu X Y, Beach K S D, Sun K, Assaad F F and Meng Z Y 2017 Phys. Rev. B 95 085110 | | [43] | Assaad F F and Grover T 2016 Phys. Rev. X 6 041049 | | [44] | Gazit S, Assaad F F, Sachdev S, Vishwanath A and Wang C 2018 Proc. Natl. Acad. Sci. USA 115 E6987 | | [45] | Gazit S, Randeria M and Vishwanath A 2017 Nat. Phys. 13 484 |
|
|
Viewed |
|
|
|
Full text
|
|
|
|
|
Abstract
|
|
|
|
|