| CONDENSED MATTER: STRUCTURE, MECHANICAL AND THERMAL PROPERTIES |
 |
|

|
|
|
Intrinsic Features of an Ideal Glass |
| Deyan Sun1,3, Cheng Shang2, Zhipan Liu2, Xingao Gong3,4** |
1Department of Physics, East China Normal University, Shanghai 200062
2Department of Chemistry, Fudan University, Shanghai 200433
3Key Laboratory for Computational Physical Sciences (MOE), State Key Laboratory of Surface Physics, Department of Physics, Fudan University, Shanghai 200433
4Collaborative Innovation Center of Advanced Microstructures, Nanjing 210093
|
|
| Cite this article: |
|
Deyan Sun, Cheng Shang, Zhipan Liu et al 2017 Chin. Phys. Lett. 34 026402 |
|
|
|
|
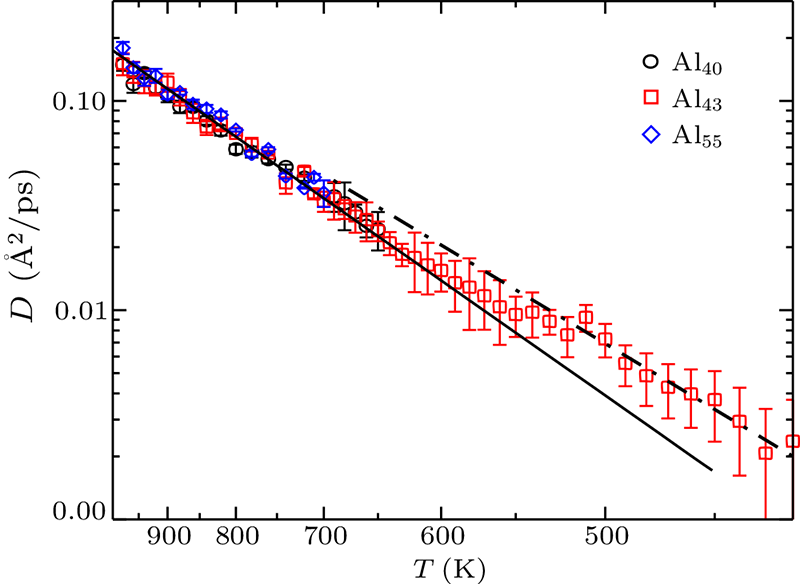
Abstract In order to understand the long-standing problem of the nature of glass states, we perform intensive simulations on the thermodynamic properties and potential energy surface of an ideal glass. It is found that the atoms of an ideal glass manifest cooperative diffusion, and show clearly different behavior from the liquid state. By determining the potential energy surface, we demonstrate that the glass state has a flat potential landscape, which is the critical intrinsic feature of ideal glasses. When this potential region is accessible through any thermal or kinetic process, the glass state can be formed and a glass transition will occur, regardless of any special structural character. With this picture, the glass transition can be interpreted by the emergence of configurational entropies, as a consequence of flat potential landscapes.
|
|
Received: 22 January 2017
Published: 25 January 2017
|
|
| PACS: |
64.70.pe
|
(Metallic glasses)
|
| |
61.43.Fs
|
(Glasses)
|
| |
61.20.Ja
|
(Computer simulation of liquid structure)
|
| |
65.80.-g
|
(Thermal properties of small particles, nanocrystals, nanotubes, and other related systems)
|
|
|
| Fund: Supported by the National Natural Science Foundation of China, and the National Basic Research Program of China. |
|
|
|
| [1] | Kennedy D and Norman C 2005 Science 309 75 | | [2] | Angell C A 1995 Science 267 1924 | | [3] | Debenedetti P G and Stillinger F H 2001 Nature 410 259 | | [4] | Berthier L and Biroli G 2011 Rev. Mod. Phys. 83 587 | | [5] | Dyre J C 2006 Rev. Mod. Phys. 78 953 | | [6] | Cavagna A 2009 Phys. Rep. 476 51 | | [7] | Wang W H 2012 Prog. Mater. Sci. 57 487 | | [8] | Micoulaut M 2016 Rep. Prog. Phys. 79 066504 | | [9] | Kauzmann W 1948 Chem. Rev. 43 219 | | [10] | Gibbs J H and DiMarzio E A 1958 J. Chem. Phys. 28 373 | | [11] | Cohen M H and Turnbull D 1959 J. Chem. Phys. 31 1164 | | [12] | Angell C A 1968 J. Am. Ceram. Soc. 51 125 | | [13] | Kirkpatrick T R, Thirumalai D and Wolynes P G 1989 Phys. Rev. A 40 1045 | | [14] | Cammarota C and Biroli G 2012 Proc. Natl. Acad. Sci. USA 109 8850 | | [15] | Sun D Y and Gong X G 1998 Phys. Rev. B 57 4730 | | [16] | Noya E G, Doye J P K and Calvo F 2006 Phys. Rev. B 73 125407 | | [17] | Neal C M, Starace A K and Jarrold M F 2007 J. Am. Soc. Mass Spectr. 18 74 | | [18] | Shang C and Liu Z P 2013 J. Chem. Theory Comput. 9 1838 | | [19] | Zhang X J, Shang C and Liu Z P 2013 J. Chem. Theory Comput. 9 3252 | | [20] | Doye J P K 2003 J. Chem. Phys. 119 1136 | | [21] | Shang C, Zhao W N and Liu Z P 2015 J. Phys.: Condens. Matter 27 134203 | | [22] | Wei G F, Shang C and Liu Z P 2015 Phys. Chem. Chem. Phys. 17 2078 | | [23] | Ercolessi F and Adams J B 1994 Europhys. Lett. 26 583 | | [24] | Sun D Y and Gong X G 2002 J. Phys.: Condens. Matter 14 L487 | | [25] | Steinhardt P J, Nelson D R and Ronchetti M 1983 Phys. Rev. B 28 784 | | [26] | Zhang X J, Shang C and Liu Z P 2017 Phys. Chem. Chem. Phys. (accepted) | | [27] | Adam G and Gibbs J H 1965 J. Chem. Phys. 43 139 | | [28] | Tombari E, Ferrari C, Salvetti G and Johari G P 2008 Phys. Rev. B 77 024304 | | [29] | Goldstein M 1969 J. Chem. Phys. 51 3728 | | [30] | Grigera T S, Cavagna A, Giardina I and Parisi G 2002 Phys. Rev. Lett. 88 055502 |
|
|
Viewed |
|
|
|
Full text
|
|
|
|
|
Abstract
|
|
|
|
|