⇦Chinese Physics Letters, 2021, Vol. 38, No. 5, Article code 054201 Broadband Terahertz Wave Generation from Monolayer Graphene Driven by Few-Cycle Laser Pulse Zhong Guan (管仲)1, Guo-Li Wang (王国利)1*, Lei Zhang (张磊)2, Zhi-Hong Jiao (焦志宏)1, Song-Feng Zhao (赵松峰)1, and Xiao-Xin Zhou (周效信)1,3* Affiliations 1College of Physics and Electronic Engineering, Northwest Normal University, Lanzhou 730070, China 2School of Mathematics and Physics, Lanzhou Jiaotong University, Lanzhou 730070, China 3Beijing National Laboratory for Condensed Matter Physics, Institute of Physics, Chinese Academy of Sciences, Beijing 100190, China Received 14 January 2021; accepted 25 February 2021; published online 2 May 2021 Supported by the National Natural Science Foundation of China (Grant Nos. 11764038, 11864037, 11765018, and 91850209).
*Corresponding authors. Email: wanggl@nwnu.edu.cn; zhouxx@nwnu.edu.cn Citation Text: Guan Z, Wang G L, Zhang L, Jiao Z H, and Zhao S F et al. 2021 Chin. Phys. Lett. 38 054201    Abstract We theoretically investigate the characteristics of terahertz (THz) radiation from monolayer graphene exposed to normal incident few-cycle laser pulses, by numerically solving the extended semiconductor Bloch equations. Our simulations show that the THz spectra in low frequency regions are highly dependent on the carrier envelope phase (CEP) of driving laser pulses. Using an optimal CEP of few-cycle laser pulses, we can obtain broadband strong THz waves, due to the symmetry breaking of the laser-graphene system. Our results also show that the strength of the THz spectra depend on both the intensity and central wavelength of the laser pulses. The intensity dependence of the THz wave can be described by the excitation rate of graphene, while wavelength dependence can be traced back to the band velocity and the population of graphene. We find that a near single-cycle THz pulse can be obtained from graphene driven by a mid-infrared laser pulse. DOI:10.1088/0256-307X/38/5/054201 © 2021 Chinese Physics Society Article Text The generation of terahertz (THz) waves has garnered a great deal of interest in recent decades, due to its wide variety of potential applications, such as large-scale object imaging, wireless communications, tomography, etc.[1–7] In addition to liquid (water,[8,9] nitrogen,[10] metal[11]), which can emit THz waves driven by lasers under some appropriate conditions as a newly emerged target, gases and crystals are two currently used types of THz-generation materials. Cook and Hochstrasser[12] first used two-color laser pulses to generate THz waves from air. The strong THz radiation from laser-induced gas plasma can be effectively explained by the photocurrent (PC) model:[13] Firstly, electrons are released via tunneling ionization, and acquire transverse moment. Next, moving electrons form a time-variant photocurrent, which finally radiates THz waves. To increase the intensity of the THz waves, three-color[14] and multi-color lasers[15] can be used as drivers. THz radiation generated in this way usually has a bandwidth of over 50 THz.[16] However, the THz waves can only be emitted when the laser intensity exceeds the ionization threshold of atoms or molecules ($\sim$$10^{14}$ W/cm$^{2}$). On the other hand, for the generation of THz wave emission from crystals driven by lasers, the most widely used methods involve the use of photoconductive antennas in semiconductors,[17] and optical rectification[18,19] in nonlinear crystals. The bandwidth of THz waves produced by both methods is approximately 5 THz or below. In recent years, with the development of ultrafast femtosecond laser technology, the few-cycle laser pulse approach has become readily available. Therefore, using crystals driven by femtosecond ultrashort laser pulses to generate THz waves has become commonplace.[20] From the perspective of current, for a crystal with non-zero bandgap, the electrons in the highest valence band are first excited to the conduction band to generate electron-hole pairs in the crystal, and the electron-hole pairs are then driven by the laser field to form a time-dependent current, thereby emitting THz waves. In general, the bandwidth of THz waves obtained from these crystals is insufficiently broad. Graphene, however, has unique properties: high electron mobility, a zero bandgap, and a wide responding frequency range. Even if the laser intensity is relatively weak ($\sim$$10^{11}$ W/cm$^{2}$), it can still induce a current in graphene.[21] Unfortunately, due to the fact that graphene is a central anti-symmetric crystal, no THz wave output has yet been observed experimentally with vertical incidence of the pump beam;[22] THz waves can be emitted only at oblique incidence.[23] It is worth noting that in experiments to date, the pulse width for the pump laser has been comparatively long (dozens of femtoseconds). In this Letter, using a few-cycle pulse as driver, thereby breaking the symmetry of the laser-graphene system, we show theoretically that graphene can radiate strong THz waves, even when laser pulse is at normal incidence on the plane of graphene. Our results show that the intensity of THz radiation depends on the carrier-envelope phase (CEP) of the few-cycle pulse, and reaches maximum when the CEP is at $\pi$/2. Compared with other crystals, we find that increased broadband THz spectra from graphene can be obtained by this method. Hence, a near single-cycle pulse can be achieved in the THz field, independent of the wavelength of the incident driving laser. Our simulations are performed by solving the extended two-band semiconductor Bloch equations (SBEs) for monolayer graphene.[24] A detailed description of this method can be found in our recent work,[25] in which we proposed an efficient theoretical approach to solving the SBEs, which avoids the divergence of the dipole transition moment near the Dirac points in graphene. For a laser field propagating perpendicular to the graphene, we obtain current near Dirac points as follows:[25] $$\begin{alignat}{1} j_{x}(t)&=v_{_{\scriptstyle \rm F}}[(\rho_{\rm cc}-\rho_{\rm vv})\cos\theta_{\boldsymbol{k}}+2\text{Im}(\rho_{\rm cv})\sin\theta_{\boldsymbol{k}}], \\ j_{y}(t)&=v_{_{\scriptstyle \rm F}}[(\rho_{\rm cc}-\rho_{\rm vv})\sin\theta_{\boldsymbol{k}}-2\text{Im}(\rho_{\rm cv})\cos\theta_{\boldsymbol{k}}],~~ \tag {1} \end{alignat} $$ where $v_{_{\scriptstyle \rm F}}=1\times 10^{6}$ m/s denotes Fermi velocity, $\rho_{\rm vv}$ and $\rho_{\rm cc}$ represent valence population and conduction population, respectively, $\rho_{\rm cv}$ is the polarization, and $\theta_{\boldsymbol{k}}$ is the directional angle of wave number $\boldsymbol{k}$.[25] Once we obtain the total integrated electric current, $\boldsymbol{J}(t)$, the THz radiation field can be calculated via a Fourier transform of the time derivative of the electron current: $$ \boldsymbol{E}_{{\rm{THz}}}(\omega)\propto\hat{F}\Big[\frac{d\boldsymbol{J}}{dt}\Big].~~ \tag {2} $$ The THz waveform in the time domain for a given frequency range can be obtained by an inverse Fourier transform of the calculated THz emission. We adopt an $x$-polarized linear laser field with the following waveform in the simulation: $$ E_{x}=E_{0}f(t)\cos(\omega t+\phi),~~ \tag {3} $$ where $E_{0}$ is the peak electric field strength, $\phi$ is the CEP, and $f(t)$ is the pulse envelope with the shape $f(t)=\cos^4(\pi t/nT)$, which gives us the zero vector potential at the end of laser pulse for different $\phi$; $nT$ is the pulse width in units of optical cycle, $T$. For such linear driving laser pulses, the integrated electric current along the $y$ direction is zero; as such, the generated THz waves are also linearly polarized. We begin by providing an example of THz emission in terms of its dependence on the symmetry of the driving laser pulse. In Fig. 1 we compare the THz spectra radiated from three-cycle laser pulses with a wavelength of $\lambda=800$ nm for two CEPs of 0 and $\pi/4$, respectively. The laser peak intensity is fixed at $5.61\times 10^{11}$ W/cm$^{2}$. It is evident that the symmetry of the laser field has a significant impact on the THz radiation strength. For $\phi=0$, the low-frequency THz radiation (considering the detecting range in this experiment, radiation levels below 10 THz constitute the main focus of our investigation; the whole bandwidth is broader than 100 THz) is very weak, whereas it is dramatically enhanced in the case of $\phi=\pi/4$.
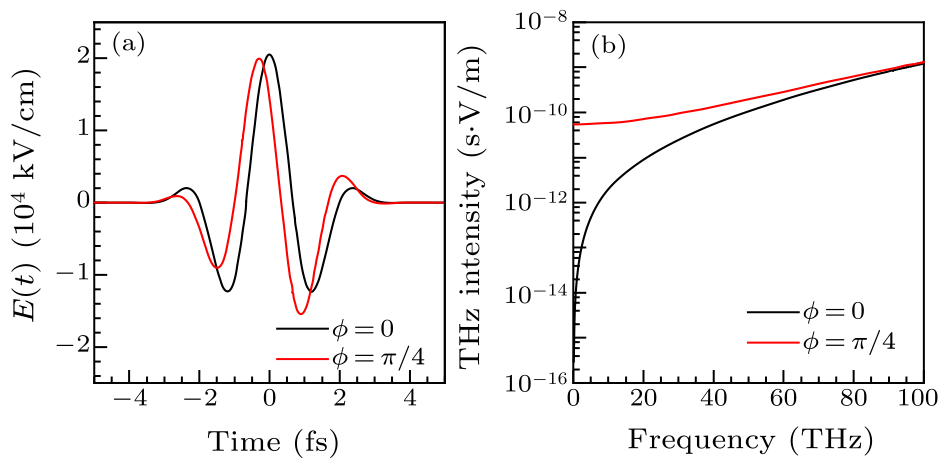
cpl-38-5-054201-fig1.png
Fig. 1. (a) Waveforms of three-cycle 800-nm laser fields for CEPs of $\phi=0$ and $\pi/4$, respectively. (b) The corresponding THz spectra generated from graphene.
cpl-38-5-054201-fig2.png
Fig. 2. Dependence of (a) low-frequency THz yield (0.1–10 THz) and (b) residual current on the CEP and width of the driving laser pulse.
In order to demonstrate systematically how the THz yield depends on the laser parameters, we show detailed simulations relating to the dependence of THz yields on the CEP and width of the driving pulse in Fig. 2. Figure 2(a) illustrates how the THz yield [$\int^{10\,\rm{THz}}_{_{\scriptstyle 0.1\,\rm{THz}}}|\boldsymbol{E}_{\rm{THz}}(\omega)|^2d\omega$] displays a periodic variation in the $\pi$ period, based on changes in the CEP. When $\phi=0$, the THz radiation is very weak, but rapidly reaches its maximum at $\phi=\pi/2$. This CEP dependence is very similar to the case of THz generation from plasma.[26] For a three-cycle pulse, the generated THz yields differ by more than two orders of magnitude between $\phi=0$ and $\phi=0.5\pi$. Such a strong CEP effect must naturally be related to laser width, as is also clearly demonstrated in Fig. 2(a). Increasing the pulse width weakens the dependence of THz radiation on the CEP. As a result, the THz emission by a longer driving laser pulse is very weak. As pulse duration increases from 3$T$ to 5$T$, the generated THz yield will decrease by about 300 times at $\phi=\pi/2$. This is consistent qualitatively with earlier experimental findings.[22] In this experiment, no THz emission is detected with the pump beam at normal incidence, when a $\sim $50-fs laser is used. Therefore, using a short-width driving pulse is crucial for the generation of strong THz radiation from graphene under a normal incident angle. We anticipate that this prediction will be confirmed experimentally in the future. Figure 2(b) further shows that these behaviors are consistent with the variation in amplitude of the residual current ($J_{x}(t$) at $t\rightarrow\infty$) at different CEPs and pulse widths, i.e., residual current reaches its maximum at $\phi=0.5\pi$, and decreases with the increasing duration of the laser pulse.
cpl-38-5-054201-fig3.png
Fig. 3. Comparison of laser waveforms and generated THz radiations for $\phi=0$ [(a), (c)] and $0.5\pi$ [(b), (d)], respectively.
cpl-38-5-054201-fig4.png
Fig. 4. Electron trajectory $k(t)$ [(c), (d)], and intra-band current $j_{_{\scriptstyle \rm{Intra}}}(t)$ [(e), (f)], induced by electrons with initial positive and negative wave numbers ($p_{x+}$ and $p_{x-}$) in a laser field with CEP values of $\phi=0$ (a) and $\phi=0.5\pi$ (b), respectively.
In order to understand how the CEP of a laser pulse affects THz radiation intensity, we consider the total THz radiation as a consequence of interference emanating from the rising and falling edges of a laser pulse. For $\phi=0$, the two parts of the laser field are symmetrical around $t=0$, and the strength of the low-frequency THz radiation from the two edges is virtually identical (see Fig. 3). Considering the phase differences between them (in the range [$\pi$, 0.95$\pi$], for radiation levels below 10 THz), coherent superposition results in a weak total radiation value. For $\phi=0.5\pi$, the laser fields from the two edges are antisymmetrical, and the phase differences between the THz fields over a wide frequency range, generated by the two edges, are very close to $\pi$. Furthermore, the THz radiation levels are far stronger due to the non-zero vector potential at $t=0$, as compared to the case of $\phi=0$. However, the difference between the THz strengths of the two edges is significant. Consequently, the total THz emission from their destructive interference is stronger than that found where $\phi=0$. The dependence of residual current on the laser field's symmetry, as shown in Fig. 2(b), can also be understood from the perspective of electron trajectory. In Figs. 4(c) and 4(d) we show two types of electron trajectory: one for an electron starting at initial negative wave number, $p_{x-}$, and the other with a positive initial wave number, $p_{x+}$. If we consider the movements of these electrons near the main peak of the laser field [the region marked by vertical dashed lines in Figs. 4(a) and  4(b); here, a single-cycle electric field is used], we find that the total summation of the contribution from $p_{x-}$ (red shaded region) and $p_{x+}$ (black shaded region) is nearly zero for $\phi=0$ and has a large non-zero value for $\phi=0.5\pi$, resulting in a weak (strong) residual intra-band current, respectively [see Figs. 4(d) and  4(e)]. Our simulations further confirm that the total THz radiation is primarily induced by the intra-band current, rather than the inter-band current, based on the following calculations: $$ \boldsymbol{J}_{\rm{intra}}(t)=\int_{_{\scriptstyle \rm BZ}}[\rho_{\rm cc}\boldsymbol{v}_{\rm c}[\boldsymbol{k}(t)]+\rho_{\rm vv}\boldsymbol{v}_{v}[\boldsymbol{k}(t)]]d\boldsymbol{k},~~ \tag {4} $$ where $\boldsymbol{v}_{\rm c}$ and $\boldsymbol{v}_{v}$ denote the band velocity from the conduction and valence bands, respectively; $\rho_{\rm cc}$ and $\rho_{\rm vv}$ denote the conduction and valence band populations, and $$\begin{alignat}{1} \boldsymbol{J}_{\rm{inter}}(t)=i\int_{_{\scriptstyle \rm BZ}}[\rho_{\rm cv}E_{\rm cv}([\boldsymbol{k}(t)]\boldsymbol{D}_{\rm cv}[\boldsymbol{k}(t)]+{\rm{c.c.}}]d\boldsymbol{k},~~ \tag {5} \end{alignat} $$ with $E_{\rm cv}(\boldsymbol{k})={E}_{\rm c}(\boldsymbol{k})-{E}_{v}(\boldsymbol{k})$, ${E}_{\rm c}$, and $E_{v}$ representing the energy band from conduction and valence bands, respectively; $\boldsymbol{D}_{\rm cv}$ is the transition dipole moment,[22] and $\rho_{\rm cv}$ refers to polarization. Next, we focus on the dependence of THz radiation on the intensity of the pump laser; the results are shown in Fig. 5. For the purpose of our calculations, we consider only laser strengths below the damage threshold of graphene. We observe that THz radiation intensity increases rapidly (slowly) under smaller (larger) laser strengths. We find that this trend can be effectively reproduced via the laser strength dependence of the tunneling rate in graphene. The low-frequency THz yield is determined by energy band population, band velocity, and inter-band polarization. At a given wave vector $k$, the band population and the inter-band polarization are related to the tunneling rate between the adiabatic states at the avoided crossings. This tunneling rate can be calculated using the Landau–Zener tunneling formula,[27] $$ P=\alpha \exp\Big(-\frac{\pi \omega_{k}^{2}}{4\mu_{k}\omega A_{0}}\Big),~~ \tag {6} $$ where $\omega_k$ denotes the energy gap, $\mu_{k}$ is the dipole moment of graphene, $\omega$ is the laser frequency, $A_{0}$ is the amplitude of vector potential, and $\alpha$ is a scaling factor. Considering Landau–Zener tunneling below $2\omega$, we find that the prediction of Eq. (4) matches very well with THz yields for different laser strengths, except for smaller strength regions, where the Landau–Zener theory fails to work.
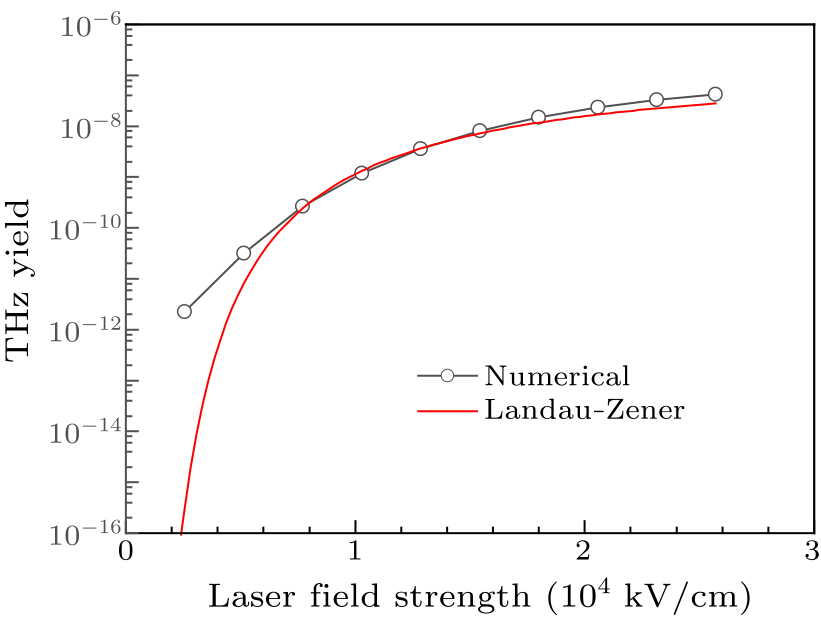
cpl-38-5-054201-fig5.png
Fig. 5. THz yield between 0.1 THz and 10 THz as a function of strength for laser pulses of 800-nm wavelength and three-cycle duration (circle). The solid line depicts the tunneling rate, calculated based on the Landau–Zener formula.
We now investigate the dependence of THz on laser wavelength. We fix the laser peak intensity at $5.61\times 10^{11}$ W/cm$^{2}$, where all pulses have the same duration, i.e., three optical cycles. Based on Fig. 6(a) it is clear that the THz radiation increases with an increase in laser wavelength, which can be scaled as $\lambda^{2.8}$. For graphene, band velocity $v_{\rm c}$ and band population are two important factors influencing low-frequency THz emission: $$ I_{\rm{{THz}}}\propto\Big\{\hat{F}\Big\{\frac{d[[\rho_{\rm cc}(t)-\rho_{\rm vv}(t)]v_{\rm c}(t)]}{dt}\Big\}\Big\}^{2}.~~ \tag {7} $$ For the sake of simplicity, we set the populations [$\rho_{\rm cc}(t)-\rho_{\rm vv}(t)$] as a constant; thus Eq. (5) can be seen as a scaled THz radiation source, based on the intra-band velocity, $v_{\rm c}(t)$. Based on our simulations, we find that the THz yield induced by $\frac{dv_{\rm c}(t)}{dt}$ scales with laser wavelength at $\lambda^{4}$ [see Fig. 6(b)], while the scaling factor $(\rho_{\rm cc}-\rho_{\rm vv})^{2}$ at the end of laser pulse ($t_\infty$) decreases with the increase in wavelength, which scales as $\lambda^{-1}$. Hence, an overall scaling factor of $\lambda^{3}$ is obtained, which is very close to the value of the complete simulation, i.e., $\lambda^{2.8}$. The dependence of THz radiation on laser intensity and wavelength shown here is qualitatively similar to the atomic case given in the literature.[28]
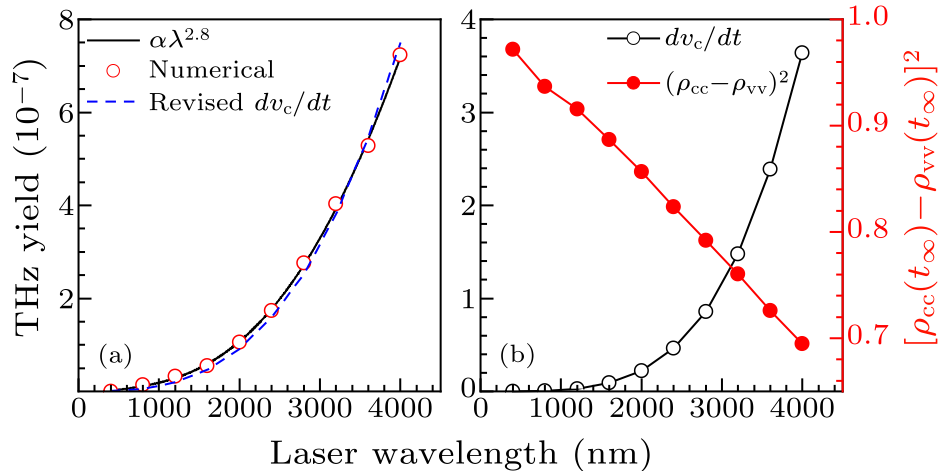
cpl-38-5-054201-fig6.png
Fig. 6. (a) THz yield below 10 THz as a function of wavelength for laser pulses of three-cycle duration (circle). The solid line is a fitting curve, the dashed line depicts the THz radiation from $(\rho_{\rm cc}-\rho_{\rm vv})\frac{dv_{\rm c}(t)}{dt}$, which scales as $\lambda^{3}$. (b) The dependence of THz yield from $\frac{dv_{\rm c}(t)}{dt}$ and $(\rho_{\rm cc}-\rho_{\rm vv})^{2}$ on the laser wavelength.
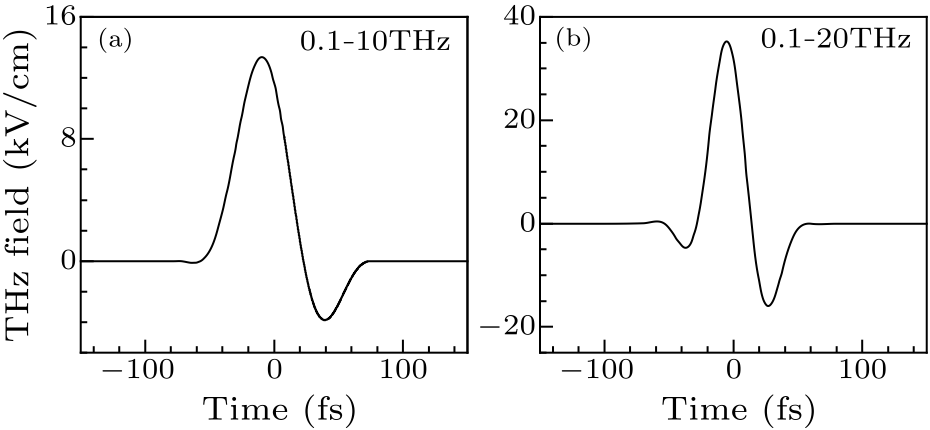
cpl-38-5-054201-fig7.png
Fig. 7. Waveforms of THz fields with a frequency range of (a) 0.1–10 THz and (b) 0.1–20 THz, generated by a three-cycle 800-nm laser pulse
Finally, we turn to the waveform of the THz electric field. Figure 7 shows the THz field at two tunable central frequencies (5 THz and 10 THz), generated by a three-cycle 800-nm laser field. It is evident that near single-cycle pulses can be obtained by superimposing THz spectra with different frequency regions. The greater the number of frequency components included, the greater the short-pulse width and high field amplitude obtained. With a longer-wavelength driving laser, a similar THz waveform can still be generated (not shown here). Moreover, the THz field amplitude can be further enhanced, while the pulse width is maintained. Such THz NSCP, due to its asymmetry electric field component, can be used in many aspects, such as the generation of Rydberg wavepacket of atoms,[29] directing the reaction coordinate of chemical reaction,[30] steering the alignment of molecule,[31] and so on. Compared to laser-plasma interaction,[32,33] the THz NSCP produced by laser-driven graphene requires a lower laser intensity. We note that these NSCPs reach a peak strength of $\sim$kV/cm, which is several orders of magnitude higher than those found in graphene excited by oblique incident laser pulses.[22,23] Using a Michelson interferometer[8] or a pyroelectric detector[34] sensitive across a wide THz range, the broadband THz radiation of over 100 THz predicted by our simulations could be detected experimentally. In summary, we have theoretically demonstrated a promising method of generating strong THz waves from graphene with femtosecond laser pulse under a normal incidence angle. Since the symmetry of the driving field has a critical impact on THz radiation intensity, we can adopt a single-color short pulse laser with only a few cycles to drive graphene. Compared with longer pulses, a THz field generated by a few-cycle laser can be rapidly enhanced by several orders of magnitude with an optimal CEP of 0.5$\pi$, and an ultrabroadband spectral bandwidth can be obtained. The THz emission dependences on the intensity and wavelength of the driving laser pulse have also been investigated, and positive scaling laws obtained, leading to the conclusion that higher laser intensities and longer wavelengths are more appropriate for the generation of stronger THz waves. Moreover, a near single-cycle THz waveform can be achieved with this method. To further break the symmetry of driving field and obtain stronger THz radiation, multi-color long femtosecond laser pulses could be used. References Materials for terahertz science and technologyTerahertz-wave sources and imaging applicationsA review of non-linear terahertz spectroscopy with ultrashort tabletop-laser pulsesJoint Measurements of Terahertz Wave Generation and High-Harmonic Generation from Aligned Nitrogen Molecules Reveal Angle-Resolved Molecular StructuresTerahertz Three-Dimensional Imaging Based on Computed Tomography with Photonics-Based Noise SourceOptical-Electrical Characteristics and Carrier Dynamics of Semi-Insulation GaAs by Terahertz Spectroscopic TechniqueRabi Oscillations and Coherence Dynamics in Terahertz Streaking-Assisted Photoelectron SpectrumHighly efficient broadband terahertz generation from ultrashort laser filamentation in liquidsObservation of broadband terahertz wave generation from liquid waterTerahertz wave generation from liquid nitrogenSingle Free-Falling Droplet of Liquid Metal as a Source of Directional Terahertz RadiationIntense terahertz pulses by four-wave rectification in airTerahertz emission from ultrafast ionizing air in symmetry-broken laser fieldsOptimized two- and three-colour laser pulses for the intense terahertz wave generationBoosting Terahertz Generation in Laser-Field Ionized Gases Using a Sawtooth Wave ShapeExtreme terahertz scienceIntense THz Pulses with large ponderomotive potential generated from large aperture photoconductive antennasHigh conversion efficiency, high energy terahertz pulses by optical rectification in cryogenically cooled lithium niobateGeneration of sub-mJ terahertz pulses by optical rectificationIntense terahertz radiation and their applicationsLight-field-driven currents in graphenePlasmon Enhanced Terahertz Emission from Single Layer GrapheneTerahertz Generation by Dynamical Photon Drag Effect in Graphene Excited by Femtosecond Optical PulsesLinking high harmonics from gases and solidsAn improved method for the investigation of high-order harmonic generation from grapheneTowards gigawatt terahertz emission by few-cycle laser pulsesHigh harmonic generation and periodic level crossingsEfficient terahertz emission by mid-infrared laser pulses from gas targetsThe dynamics of a THz Rydberg wavepacketTHz-Pulse-Induced Selective Catalytic CO Oxidation on RuField-free alignment dynamics of FCN molecule induced by a terahertz half-cycle pulseHalf-cycle-pulse terahertz emission from an ultrafast laser plasma in a solid targetControlling of strong tunable THz emission with optimal incommensurate multi-color laser fieldTerahertz pulse generation by two-color laser fields with circular polarization
[1] Ferguson B and Zhang X C 2002 Nat. Mater. 1 26
[2] Dobroiu D, Otani C, and Kawase K 2006 Meas. Sci. Technol. 17 R161
[3] Hwang H Y, Fleischer S, Brandt N C, Perkins J B G, Liu M, Fan K, Sternbach A, Zhang X, Averitt R D, and Nelson K A 2015 J. Mod. Opt. 62 1447
[4] Huang Y, Meng C, Wang X, Lü Z, Zhang D, Chen W, Zhao J, Yuan J, and Zhao Z 2015 Phys. Rev. Lett. 115 123002
[5] Zhou T, Zhang R, Yao C, Fu Z L, Shao S X, and Cao J C 2017 Chin. Phys. Lett. 34 084206
[6] Han X W, Hou L, Yang L, Wang Z Q, Zhao M M, and Shi W 2016 Chin. Phys. Lett. 33 120701
[7] Wang S, Zhu Z, Zhang Y, Yan T M, and Jiang Y 2021 Chin. Phys. Lett. 38 013401
[8] Dey I, Jana K, Fedorov A D, Yu W V, Koulouklidis A D, Mondal A, Shaikh M, Sarkar D, Lad A D, Tzortzakis S, Couairon A, and Kumar G R 2017 Nat. Commun. 8 1184
[9] Jin Q, Yiwen E, Williams K, Dai J, and Zhang X C 2017 Appl. Phys. Lett. 111 071103
[10] Balakin A V, Coutaz J L, Makarov V A, Kotelnikov I A, Peng Y, Solyankin P M, Zhu Y, and Shkurinov A P 2019 Photon. Res. 7 678
[11] Solyankin P M, Lakatosh B V, Krivokorytov M S, Tsygvintsev I P, Sinko A S, Kotelnikov I A, Makarov V A, Coutaz J L, Medvedev V V, and Shkurinov A P 2020 Phys. Rev. Appl. 14 034033
[12] Cook D J and Hochstrasser R M 2000 Opt. Lett. 25 1210
[13] Kim K Y, Glownia J H, Taylor A J, and Rodriguez G 2007 Opt. Express 15 4577
[14] Zhang L, Wang G L, and Zhou X X 2016 J. Mod. Opt. 63 2159
[15] de González A M P, Babushkin I, Bergé L, Skupin S, Cabrera-Granado E, Köhler C, Morgner U, Husakou A, and Herrmann J 2015 Phys. Rev. Lett. 114 183901
[16] Zhang X C, Shkurinov A, and Zhang Y 2017 Nat. Photon. 11 16
[17] Ropagnol X, Khorasaninejad M, Raeiszadeh M, Safavi-Naeini S, Bouvier M, Côté C Y, Laramée A, Reid M, Gauthier M A, and Ozaki T 2016 Opt. Express 24 11299
[18] Huang S W, Granados E, Huang W R, Hong K H, Zapata L E, and Kärtner F X 2013 Opt. Lett. 38 796
[19] Fülöp J A, Palfalvi L, Klingebiel S, Almási G, Krausz F, Karsch S, and Hebling J 2012 Opt. Lett. 37 557
[20] Hafez H A, Chai X, Ibrahim A, Mondal S, Férachou D, Ropagnol X, and Ozaki T 2016 J. Opt. 18 093004
[21] Higuchi T, Heide C, Ullmann K, Weber H B, and Hommelhoff P 2017 Nature 550 224
[22] Bahk Y M, Ramakrishnan G, Choi J, Song H, Choi G, Kim Y H, Ahn K J, Kim D S, and Planken P C M 2014 ACS Nano 8 9089
[23] Maysonnave J, Huppert S, Wang F, Maero S, Berger C, de Heer W, Norris T B, De Vaulchier L A, Dhillon S, Tignon J, Ferreira R, and Mangeney J 2014 Nano Lett. 14 5797
[24] Vampa G, Hammond T J, Thiré N, Schmidt B E, Légaré F, McDonald C R, Brabec T, and Corkum P B 2015 Nature 522 462
[25] Guan Z, Liu L, Wang G L, Zhao S F, Jiao Z H, and Zhou X X 2020 Chin. Phys. B 29 104206
[26] Wang W M, Kawata S, Sheng Z M, Li Y T, and Zhang J 2011 Phys. Plasmas 18 073108
[27] Gauthey F I, Garraway B M, and Knight P L 1997 Phys. Rev. A 56 3093
[28] Wang W M, Kawata S, Sheng Z M, Li Y T, Zhang J, Chen L M, Qian L J, and Zhang J 2011 Opt. Lett. 36 2608
[29] Wetzels A, Gürtler A, Muller H G, and Noordam L D 2001 Eur. Phys. J. D 14 157
[30] LaRue J L, Katayama T, Lindenberg A, Fisher A S, Öström H, Nilsson A, and Ogasawara H 2015 Phys. Rev. Lett. 115 036103
[31] Cheng Q Y, Liu J S, Zhou X C, Song Y Z, and Meng Q T 2019 Europhys. Lett. 125 33001
[32] Gao Y, Drake T, Chen Z, and DeCamp M F 2008 Opt. Lett. 33 2776
[33] Zhang L, Wang G L, Zhao S F, and Zhou X X 2017 Phys. Plasmas 24 023116
[34] Tailliez C, Stathopulos A, Skupin S, Buožius D, Babushkin I, Vaičaitis V, and Bergé L 2020 New J. Phys. 22 103038