| THE PHYSICS OF ELEMENTARY PARTICLES AND FIELDS |
|

|
|
|
Valence Quark Ratio in the Proton |
| Zhu-Fang Cui1,2, Fei Gao3, Daniele Binosi4*, Lei Chang5*, Craig D. Roberts1,2*, and Sebastian M. Schmidt6,7 |
1School of Physics, Nanjing University, Nanjing 210093, China
2Institute for Nonperturbative Physics, Nanjing University, Nanjing 210093, China
3Centre for High Energy Physics, Peking University, Beijing 100871, China
4European Centre for Theoretical Studies in Nuclear Physics and Related Areas, Villa Tambosi, Strada delle Tabarelle 286, I-38123 Villazzano (TN), Italy
5School of Physics, Nankai University, Tianjin 300071, China
6Helmholtz-Zentrum Dresden-Rossendorf, Dresden D-01314, Germany
7RWTH Aachen University, III. Physikalisches Institut B, Aachen D-52074, Germany
|
|
| Cite this article: |
|
Zhu-Fang Cui, Fei Gao, Daniele Binosi et al 2022 Chin. Phys. Lett. 39 041401 |
|
|
|
|
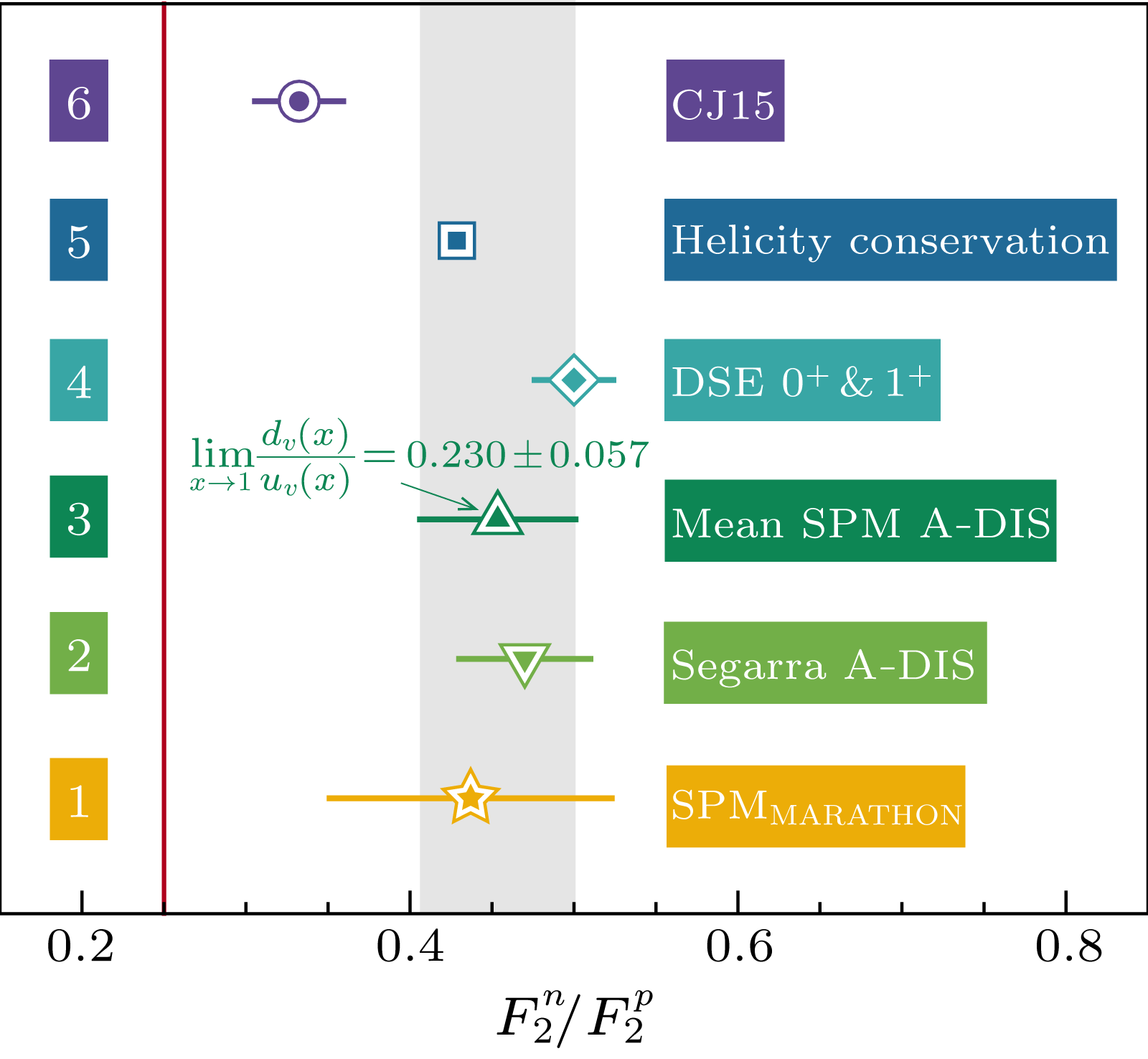
Abstract Beginning with precise data on the ratio of structure functions in deep inelastic scattering (DIS) from $^3$He and $^3$H, collected on the domain $0.19 \leq x_{\scriptscriptstyle{\rm B}} \leq 0.83$, where $x_{\scriptscriptstyle{\rm B}}$ is the Bjorken scaling variable, we employ a robust method for extrapolating such data to arrive at a model-independent result for the $x_{\scriptscriptstyle{\rm B}}=1$ value of the ratio of neutron and proton structure functions. Combining this with information obtained in analyses of DIS from nuclei, corrected for target-structure dependence, we arrive at a prediction for the proton valence-quark ratio: $\left. d_v/u_v \right|_{x_{\scriptscriptstyle{\rm B}}\to 1} = 0.230 (57)$. Requiring consistency with this result presents a challenge to many descriptions of proton structure.
|
|
Received: 19 March 2022
Express Letter
Published: 24 March 2022
|
|
| PACS: |
14.20.Dh
|
(Protons and neutrons)
|
| |
13.60.Hb
|
(Total and inclusive cross sections (including deep-inelastic processes))
|
| |
12.38.Aw
|
(General properties of QCD (dynamics, confinement, etc.))
|
|
|
|
|
|
| [1] | Gell-Mann M 1964 Phys. Lett. 8 214 |
| [2] | Zweig G 1964 CERN Rep. Nos. 8182/TH.401 and 8419/TH.412 |
| [3] | Lucha W, Schöberl F F, and Gromes D 1991 Phys. Rep. 200 127 |
| [4] | Capstick S and Roberts W 2000 Prog. Part. Nucl. Phys. 45 S241 |
| [5] | Giannini M M and Santopinto E 2015 Chin. J. Phys. 53 020301 |
| [6] | Roberts C D, Richards D G, Horn T, and Chang L 2021 Prog. Part. Nucl. Phys. 120 103883 |
| [7] | Brodsky S J and Lepage G P 1989 Adv. Ser. Direct. High Energy Phys. 5 93 |
| [8] | Ellis R K, Stirling W J, and Webber B R 2011 QCD and Collider Physics (Cambridge: University Press) |
| [9] | Holt R J and Roberts C D 2010 Rev. Mod. Phys. 82 2991 |
| [10] | Rojo J et al. 2015 J. Phys. G 42 103103 |
| [11] | Peng J C and Qiu J W 2018 Universe 4 34 |
| [12] | Hen O, Miller G A, Piasetzky E, and Weinstein L B 2017 Rev. Mod. Phys. 89 045002 |
| [13] | Bjorken J D 1969 Phys. Rev. 179 1547 |
| [14] | Taylor R E 1991 Rev. Mod. Phys. 63 573 |
| [15] | Friedman J I 1991 Rev. Mod. Phys. 63 615 |
| [16] | Kendall H W 1991 Rev. Mod. Phys. 63 597 |
| [17] | Friedman J I, Kendall H W, and Taylor R E 1991 Rev. Mod. Phys. 63 629 |
| [18] | Roberts C D, Holt R J, and Schmidt S M 2013 Phys. Lett. B 727 249 |
| [19] | Dirac P A M 1949 Rev. Mod. Phys. 21 392 |
| [20] | Kogut J B and Soper D E 1970 Phys. Rev. D 1 2901 |
| [21] | Bjorken J D, Kogut J B, and Soper D E 1971 Phys. Rev. D 3 1382 |
| [22] | Bodek A, Breidenbach M, Dubin D L, Elias J E, Friedman J I, Kendall H W, Poucher J S, Riordan E M, Sogard M R, and Coward D H 1973 Phys. Rev. Lett. 30 1087 |
| [23] | Poucher J S et al. 1974 Phys. Rev. Lett. 32 118 |
| [24] | Abrams D et al. 2022 Phys. Rev. Lett. (in press) |
| [25] | Dove J et al. 2021 Nature 590 561 |
| [26] | Zyla P et al. 2020 Prog. Theor. Exp. Phys. 2020 083C01 |
| [27] | Chang L and Roberts C D 2021 Chin. Phys. Lett. 38 081101 |
| [28] | Chang L, Gao F, and Roberts C D 2022 arXiv:2201.07870 [hep-ph] |
| [29] | Nachtmann O 1973 Nucl. Phys. B 63 237 |
| [30] | Cui Z F, Ding M, Gao F, Raya K, Binosi D, Chang L, Roberts C D, Rodrı́guez-Quintero J, and Schmidt S M 2021 Eur. Phys. J. A 57 5 |
| [31] | Cockroft J D and Walton E T S 1932 Proc. R. Soc. London Ser. A 136 619 |
| [32] | Whitlow L W, Riordan E M, Dasu S, Rock S, and Bodek A 1992 Phys. Lett. B 282 475 |
| [33] | Afnan I R, Bissey F R P, Gomez J, Katramatou A T, Melnitchouk W, Petratos G G, and Thomas A W 2000 Phys. Lett. B 493 36 |
| [34] | Pace E, Salme G, Scopetta S, and Kievsky A 2001 Phys. Rev. C 64 055203 |
| [35] | Segarra E, Schmidt A, Kutz T, Higinbotham D, Piasetzky E, Strikman M, Weinstein L, and Hen O 2020 Phys. Rev. Lett. 124 092002 |
| [36] | Segarra E P et al. 2021 arXiv:2104.07130 [hep-ph] |
| [37] | Cocuzza C, Keppel C E, Liu H, Melnitchouk W, Metz A, Sato N, and Thomas A W 2021 Phys. Rev. Lett. 127 242001 |
| [38] | Schlessinger L 1968 Phys. Rev. 167 1411 |
| [39] | Schlessinger L and Schwartz C 1966 Phys. Rev. Lett. 16 1173 |
| [40] | Tripolt R A, Haritan I, Wambach J, and Moiseyev N 2017 Phys. Lett. B 774 411 |
| [41] | Chen C, Lu Y, Binosi D, Roberts C D, Rodrı́guez-Quintero J, and Segovia J 2019 Phys. Rev. D 99 034013 |
| [42] | Binosi D, Chang L, Ding M, Gao F, Papavassiliou J, and Roberts C D 2019 Phys. Lett. B 790 257 |
| [43] | Binosi D and Tripolt R A 2020 Phys. Lett. B 801 135171 |
| [44] | Eichmann G, Duarte P, Peña M T, and Stadler A 2019 Phys. Rev. D 100 094001 |
| [45] | Yao Z Q, Binosi D, Cui Z F, Roberts C D, Xu S S, and Zong H S 2020 Phys. Rev. D 102 014007 |
| [46] | Yao Z Q, Binosi D, Cui Z F, and Roberts C D 2021 Phys. Lett. B 818 136344 |
| [47] | Yao Z Q, Binosi D, Cui Z F, and Roberts C D 2022 Phys. Lett. B 824 136793 |
| [48] | Cui Z F, Binosi D, Roberts C D, and Schmidt S M 2021 Phys. Rev. Lett. 127 092001 |
| [49] | Cui Z F, Binosi D, Roberts C D, and Schmidt S M 2021 Phys. Lett. B 822 136631 |
| [50] | Cui Z F, Binosi D, Roberts C D, and Schmidt S M 2021 Chin. Phys. Lett. 38 121401 |
| [51] | Reinsch C H 1967 Numer. Math. 10 177 |
| [52] | Press W H, Teukolsky S A, Vetterling W T, and Flannery B P 2007 Numerical Recipes 3rd edn The Art of Scientific Computing (New York: Cambridge University Press) |
| [53] | Accardi A, Brady L T, Melnitchouk W, Owens J F, and Sato N 2016 Phys. Rev. D 93 114017 |
| [54] | Xiong W et al. 2019 Nature 575 147 |
| [55] | Norton P R 2003 Rep. Prog. Phys. 66 1253 |
| [56] | Arrington J, Higinbotham D W, Rosner G, and Sargsian M 2012 Prog. Part. Nucl. Phys. 67 898 |
| [57] | Segovia J, Cloet I C, Roberts C D, and Schmidt S M 2014 Few-Body Syst. 55 1185 |
| [58] | Xu S S, Chen C, Cloet I C, Roberts C D, Segovia J, and Zong H S 2015 Phys. Rev. D 92 114034 |
| [59] | Farrar G R and Jackson D R 1975 Phys. Rev. Lett. 35 1416 |
| [60] | Brodsky S J, Burkardt M, and Schmidt I 1995 Nucl. Phys. B 441 197 |
| [61] | Close F E and Thomas A W 1988 Phys. Lett. B 212 227 |
| [62] | Anselmino M, Predazzi E, Ekelin S, Fredriksson S, and Lichtenberg D B 1993 Rev. Mod. Phys. 65 1199 |
| [63] | Barabanov M Y et al. 2021 Prog. Part. Nucl. Phys. 116 103835 |
| [64] | Roberts C D 2020 Symmetry 12 1468 |
| [65] | Eichmann G, Alkofer R, Krassnigg A, and Nicmorus D 2010 Phys. Rev. Lett. 104 201601 |
| [66] | Eichmann G 2011 Phys. Rev. D 84 014014 |
| [67] | Qin S X, Roberts C D, and Schmidt S M 2019 Few-Body Syst. 60 26 |
|
|
Viewed |
|
|
|
Full text
|
|
|
|
|
Abstract
|
|
|
|
|