⇦Chinese Physics Letters, 2022, Vol. 39, No. 9, Article code 097501 Magneto-Elastic Coupling in a Sinusoidal Modulated Magnet Cr$_2$GaN Hui-Can Mao (毛慧灿)1,2, Yu-Feng Li (李玉峰)3, Qing-Yong Ren (任清勇)4,5, Mi-Hai Chu (褚密海)6, Helen E. Maynard-Casely7, Franz Demmel8, Devashibhai Adroja8, Hai-Hu Wen (闻海虎)3, Yin-Guo Xiao (肖荫果)6*, and Hui-Qian Luo (罗会仟)1,9* Affiliations 1Beijing National Laboratory for Condensed Matter Physics, Institute of Physics, Chinese Academy of Sciences, Beijing 100190, China 2University of Chinese Academy of Sciences, Beijing 100049, China 3National Laboratory of Solid State Microstructures and Department of Physics, Collaborative Innovation Center of Advanced Microstructures, Nanjing University, Nanjing 210093, China 4Institute of High Energy Physics, Chinese Academy of Sciences, Beijing 100049, China 5Spallation Neutron Source Science Center, Dongguan 523803, China 6School of Advanced Materials, Shenzhen Graduate School, Peking University, Shenzhen 518055, China 7Australian Centre for Neutron Scattering, Australian Nuclear Science and Technology Organisation, Lucas Heights NSW-2232, Australia 8ISIS Facility, Rutherford Appleton Laboratory, Chilton, Didcot Oxon OX11 0QX, United Kingdom 9Songshan Lake Materials Laboratory, Dongguan 523808, China Received 28 June 2022; accepted manuscript online 27 July 2022; published online 12 August 2022 *Corresponding authors. Email: y.xiao@pku.edu.cn; hqluo@iphy.ac.cn Citation Text: Mao H C, Li Y F, Ren Q Y et al. 2022 Chin. Phys. Lett. 39 097501    Abstract We use neutron powder diffraction to investigate the magnetic and crystalline structure of Cr$_2$GaN. A magnetic phase transition is identified at $T \approx 170$ K, whereas no trace of structural transition is observed down to 6 K. Combining Rietveld refinement with irreducible representations, the spin configuration of Cr ions in Cr$_2$GaN is depicted as an incommensurate sinusoidal modulated structure characterized by a propagating vector $k=(0.365, 0.365, 0)$. Upon warming up to the paramagnetic state, the magnetic order parameter closely resembles to the temperature dependence of $c$-axis lattice parameter, suggesting strong magneto-elastic coupling in this compound. Therefore, Cr$_2$GaN provides a potential platform for exploration of magnetically tuned properties such as magnetoelectric, magnetostrictive and magnetocaloric effects, as well as their applications.
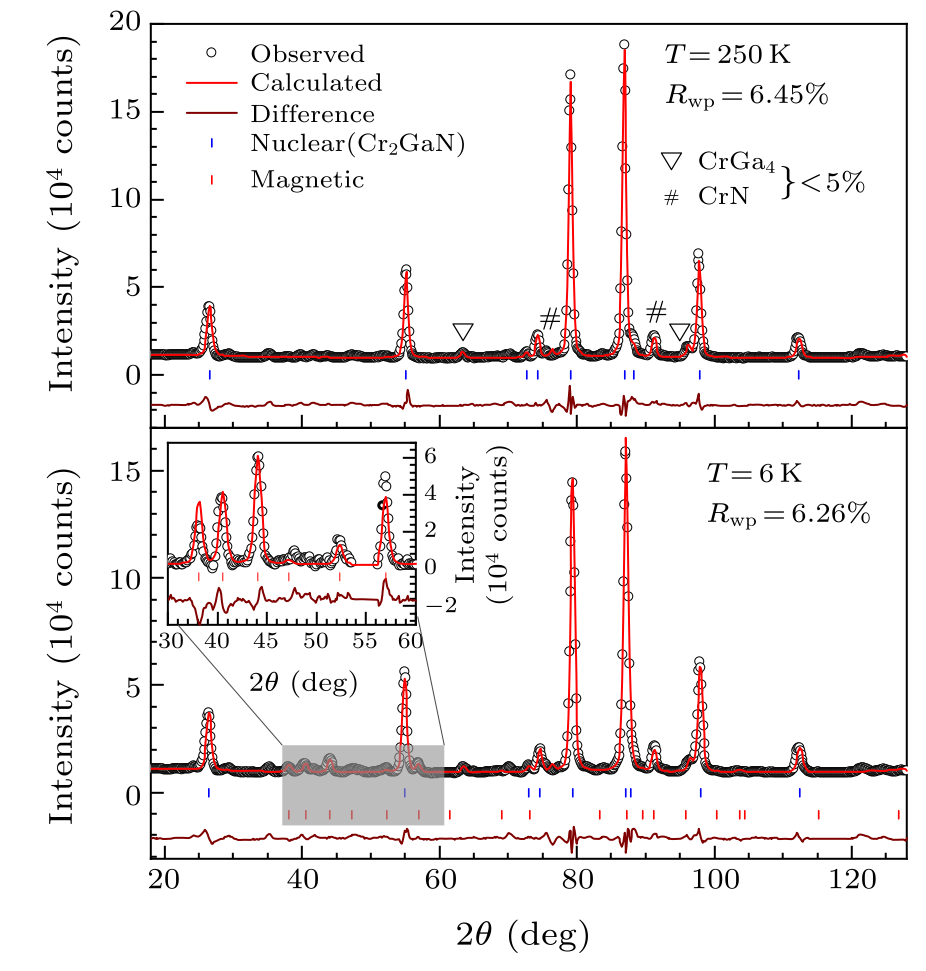
cpl-39-9-097501-fig1.png
cpl-39-9-097501-fig2.png
cpl-39-9-097501-fig3.png
 DOI:10.1088/0256-307X/39/9/097501 © 2022 Chinese Physics Society Article Text The M$_{n+1}$AX$_n$ (MAX) phases, crystallized in hexagonal $P6_3/mmc$, where M is a transition metal element, A is an IIIA or IVA group element, X is either C or N and $n$ varies from 1 to 3, have attracted considerable interest for a unique combination of metallic properties such as good electrical conductivity, and ceramic properties like high elastic moduli.[1-3] The MAX compounds are composed of near-close-packed layers of M$_6$X octahedra interleaved with layers of pure A atoms. These MAX phases are extremely resistant to oxidation and thermal shock, elastically stiff, while at the same time they exhibit high electrical and thermal conductivity which are machinable.[4,5] In addition to the unique metallic and ceramic characters in inherently nanolaminated MAX phases, magnetism characterized by high stability and tunable anisotropic properties are fascinating for both fundamental materials science and practical applications, such as spintronics manipulated by the interlayer exchange coupling, and metallic magnetism realized in the geometrically frustrated two-dimensional plane.[6-10] Mostly magnetic MAX phases reported to date, either in bulk or thin film form, are composed of Cr or Mn as transition metal elements.[6] The significantly correlated nature of the $d$ orbitals of Cr and Mn in MAX compounds generates diverse magnetic interactions under either ferromagnetic (FM) or antiferromagnetic (AFM) order, which strongly depend on the chemical composition and other tuning parameters such as temperature and pressure. For example, Cr$_2$GeC is probably located in the vicinity of an FM quantum critical point, whereas the Mn-doped Cr$_2$GeC shows itinerant-electron ferromagnetism in a wide range of the degree of electron localization.[11] Interestingly, Mn$_2$GaC undergoes a magnetic transition ($\sim $210 K) from a collinear AFM state to a non-collinear AFM configuration due to the spin reorientation, accompanied by a $c$-axis lattice compression with decreasing temperature.[7,8] This suggests a strong coupling between spin and lattice, so called “magneto-elastic” coupling, in the layered MAX phase. Such rich magnetic properties in MAX phases open a pathway to explore new functionalities for spintronic, magnetoelectric and magnetocaloric applications by enabling the manipulation of electronic, magnetic and crystalline structure. Analogously, a spin-density-wave (SDW) transition has been found in MAX phase Cr$_2$GaN at $T_{\rm N} = 170$ K by measuring the zero-field muon spin relaxation (ZF-$\mu$SR), magnetic susceptibility and resistivity.[12,13] Furthermore, nuclear magnetic resonance (NMR) experiments suggest that the static and distributed internal field is expected for the frustrated magnetism or incommensurate SDW state[13] in Cr$_2$GaN. Such rich and complicated magnetic properties in Cr$_2$GaN will inspire us to determine its magnetic ground state and further to explore the interactions between spin and lattice by neutron diffraction experiments.
cpl-39-9-097501-fig1.png
Fig. 1. The Rietveld refinement results with hexagonal phase $P6_3/mmc$ at (a) 250 K and (b) 6 K. The vertical blue lines represent the positions of the Bragg peaks in Cr$_2$GaN, red lines designate those of magnetic peaks, inverted triangle is the impurities of CrGa$_4$ and CrN. The inset in Fig. 1(b) gives a schematic show of the refinement of magnetic phase in the range of 2${\theta} \sim 35^{\circ}$–60$^{\circ}$.
The polycrystalline samples of Cr$_2$GaN were synthesized by the solid state reaction method as described in Ref. [12]. Neutron powder diffraction experiments were carried out on both OSIRIS high-resolution diffractometer at ISIS facility, STFC Rutherford Appleton Laboratory (Proposal No. RB1610019) and WOMBAT high-intensity diffractometer at Australian Nuclear Science and Technology Organisation (Proposal No. P6014) with wavelength $\lambda = 2.95$ Å. To obtain diffraction data with good counting statistics and homogeneous background, about 5 g of Cr$_2$GaN powders were laid flat between two layers of aluminum foil, then rolled up and placed against the wall of Aluminum can for the experiment at OSIRIS diffractometer, whereas the same batch of samples $\sim $5 g were sealed in a vanadium can at WOMBAT diffractometer. The full pattern measurements were conducted on WOMBAT diffractometer at 6 K and 250 K by covering the scattering angle $2\theta$ from 15$^\circ$ to 136$^\circ$, whereas the temperature-dependent diffraction data ranging from 10 K to 250 K were collected at OSIRIS diffractometer with interplanar $d$-spacing from 3.1 to 5.3 Å, including a nuclear reflection (004) and several magnetic reflections. For the structural refinement, we focus on the WOMBAT data using Rietveld method and irreducible representation theory embedded in the FullProf[14,15] and SARAH[16] software package. The raw data of neutron diffraction patterns at 250 K and 6 K obtained from WOMBAT diffractometer are presented in Fig. 1. To quantitatively analyze the crystal structure and magnetic structure of Cr$_2$GaN, we have performed the Rietveld refinement for these two data sets. The majority of Bragg reflections can be indexed by a hexagonal phase of Cr$_2$GaN with space group $P6_3/mmc$ for both patterns at 250 K and 6 K, whereas some weak reflections indicate the existence of very small amounts of CrGa$_4$ and CrN impurity phases (<5%) [Fig. 1(a)]. The parameters for the quality of this two fittings, including profile factor $R_{\rm p}$ and weighted profile factor $R_{\rm wp}$, are 4.75(3), 6.44(5) at 250 K and 4.88(4), 6.45(3) at 6 K, respectively. All crystallographic parameters listed in Table 1 are mostly consistent with the previous x-ray diffraction results.[12] Since both data sets at 250 K and 6 K can be fully identified with the same space group $P6_3/mmc$, we thus conclude that there is no observable structural phase transition in Cr$_2$GaN down to 6 K. As illustrated in Fig. 1(b), a few magnetic peaks emerge at low temperature of 6 K ranging from 35$^{\circ}$ to 60$^{\circ}$, indicating the formation of a long-rang magnetic order in Cr$_2$GaN. All magnetic peaks at 6 K can be well indexed with a propagation vector $k = (0.365, 0.365, 0)$, suggesting an incommensurate magnetic structure.
Table 1. Crystallographic data of Cr$_2$GaN at 250 K and 6 K.
250 K 6 K
Space group $P6_3/mmc$ $P6_3/mmc$
$a$ (Å) 2.861(5) 2.850(1)
$c$ (Å) 12.671(9) 12.713(1)
$z_{_{\scriptstyle \rm Cr}}$ 0.087(2) 0.089(1)
B$_{\rm iso}$(Cr) (Å$^{2}$) 1.118(2) 0.350(1)
B$_{\rm iso}$(Ga) (Å$^{2}$) 0.839(2) 0.515(8)
B$_{\rm iso}$(N) (Å$^{2}$) 1.112(6) 0.960(8)
Atom Wyckoff $x$ $y$ $z$
Cr $4f$ 1/3 2/3 $z_{_{\scriptstyle \rm Cr}}$
Ga $2d$ 1/3 2/3 0.75
N $2a$ 0 0 0
The magnetic symmetry analysis for Cr$_2$GaN is performed using the program SARAH, by which the allowed symmetry coupling in the form of irreducible representation (IR) and their basis vectors (BVs) can be obtained. With the incommensurate magnetic propagation vector $k = (0.365, 0.365, 0)$, the Cr ion occupying at crystallographic Wyckoff site ($4f$) has four one-dimensional irreducible magnetic representations including $\varGamma_1$, $\varGamma_2$, $\varGamma_3$ and $\varGamma_4$, and each of them has three basis vectors with only real components. To determine the magnetic structure of Cr$_2$GaN, we use all possible IRs in the magnetic structural model to fit the neutron diffraction pattern at 6 K. We find that irreducible representation $\varGamma_3$ is the best fitting of all magnetic peaks, whereas the other three representations can be excluded due to poor fits of magnetic peaks. The decomposition of the magnetic representation $\varGamma_3$ is given in Table 2. According to $\varGamma_3$, the Cr moments are ordered in a sinusoidal structure in the magnetic unit cell and the refined vector components of the magnetic moment are $m_x = 0.4\,{\mu}_{\scriptscriptstyle{\rm B}}$, $m_y = -0.05\,{\mu}_{\scriptscriptstyle{\rm B}}$ and $m_z = 1.5\,{\mu}_{\scriptscriptstyle{\rm B}}$. The Cr ion at $4f$ Wyckoff site has 4 equivalent Cr ions in the unit cell marked with Cr1(0.333, 0.667, 0.089), Cr2(0.667, 0.333, 0.911), Cr3(0.333, 0.667, 0.411), and Cr4(0.667, 0.333, 0.589) in Fig. 2(a), and their ($m_x$, $m_y$, $m_z$) are (0.4, $-0.05$, 1.5) ${\mu}_{\scriptscriptstyle{\rm B}}$, (0.05, $-0.4$, 1.5) ${\mu}_{\scriptscriptstyle{\rm B}}$, ($-0.4$, 0.05, 1.5) ${\mu}_{\scriptscriptstyle{\rm B}}$, and ($-0.05$, 0.4, 1.5) ${\mu}_{\scriptscriptstyle{\rm B}}$, respectively. It is clear that the magnetic moment components of Cr ions are lying in $a$–$c$ and $b$–$c$ planes. More precisely, we note that Cr1 and Cr3 moments in $a$–$c$ plane (or Cr2 and Cr4 in $b$–$c$ plane) form a sinusoidal wave modulated structure model along $a$-axis (or $b$-axis) as shown in Figs. 2(b) and 2(c), respectively. The estimated value of the total ordered moment is about 1.56${\mu}_{\scriptscriptstyle{\rm B}}$, which is slightly larger than the reported results of ${\mu}$SR experiments ($ < 1 \mu_{\scriptscriptstyle{\rm B}}$).[13]
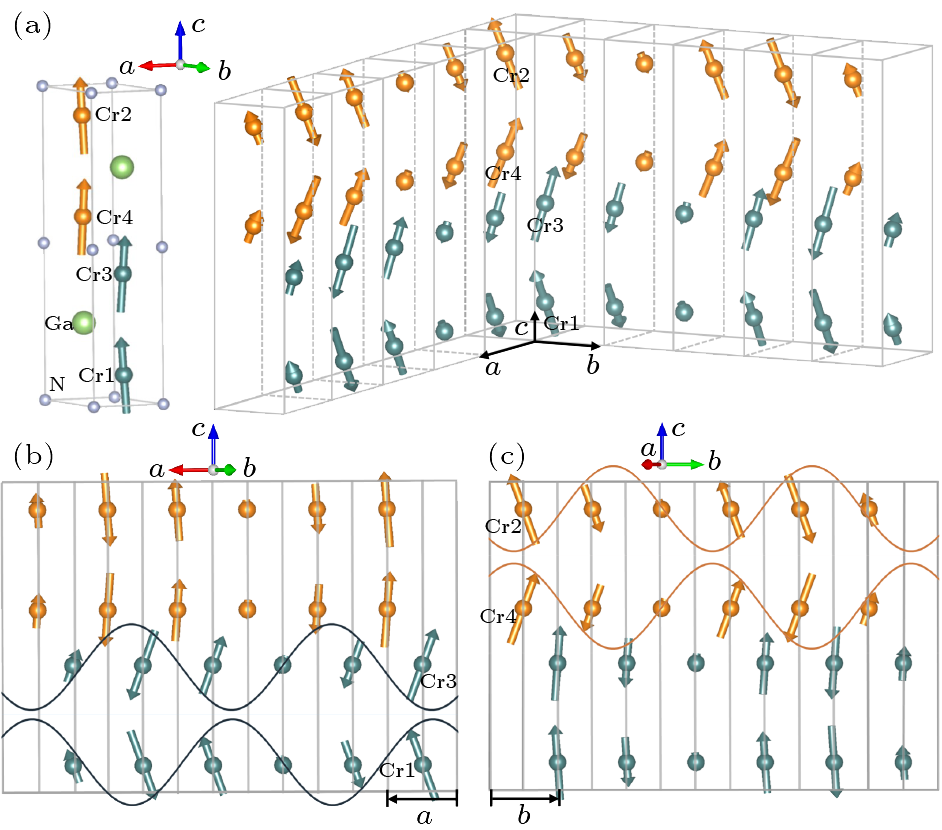
cpl-39-9-097501-fig2.png
Fig. 2. (a) Three-dimensional sinusoidal modulated magnetic structure of Cr$_2$GaN at 6 K in single unit cell and supercell. Two-dimensional sinusoidal modulated magnetic structure of Cr$_2$GaN at 6 K along (b) $a$-axis and (c) $b$-axis.
Table 2. Nonzero basis vectors (BVs) of the irreducible representations (IRs) and positional coordinates for Cr atoms that are used to describe the sinusoidal modulated magnetic structure of Cr$_2$GaN with space group $P6_3/mmc$ and propagation vector $k = (0.365, 0.365, 0)$.
BV components Positional coordinates
IR BV Atom $m_{||a}$ $m_{||b}$ $m_{||c}$ $x$ $y$ $z$
$\varGamma_3$ $\psi_7$ 1 1 0 0 $x$ $y$ $z$
2 0 $-1$ 0 ${\bar{x}}$+1 ${\bar{y}}$+1 ${\bar{z}}$+1
3 $-1$ 0 0 $x$ $y$ ${\bar{z}}+1/2$
4 0 1 0 ${\bar{x}}$+1 ${\bar{y}}$+1 $z+1/2$
$\psi_8$ 1 0 1 0 $x$ $y$ $z$
2 $-1$ 0 0 ${\bar{x}}$+1 ${\bar{y}}$+1 ${\bar{z}}$+1
3 0 $-1$ 0 $x$ $y$ ${\bar{z}}+1/2$
4 1 0 0 ${\bar{x}}$+1 ${\bar{y}}$+1 $z+1/2$
$\psi_9$ 1 0 0 1 $x$ $y$ $z$
2 0 0 1 ${\bar{x}}$+1 ${\bar{y}}$+1 ${\bar{z}}$+1
3 0 0 1 $x$ $y$ ${\bar{z}}+1/2$
4 0 0 1 ${\bar{x}}$+1 ${\bar{y}}$+1 $z+1/2$
Now we turn to the diffraction pattern covering interplanar distance $d \sim 3.1$–4.65 Å as shown in Fig. 3, obtained from OSIRIS diffractometer with measured temperatures range from 10 K to 250 K. In Fig. 3(a), the four magnetic peaks (002)$_{\rm M} \pm k$, (000)$_{\rm M} \pm k$, (101)$_{\rm M}-k$, and (100)$_{\rm M}-k$, centered around 3.32 Å, 3.85 Å, 4.28 Å, and 4.48 Å, gradually become weaker with increasing temperature and disappear completely above magnetic phase transition temperature $T_{\rm M}\approx 170$ K. Notably, the positions of all magnetic peaks shift upon warming up to $T_{\rm M}$, so does the position of (004) nuclear peak. As both the magnetic and crystalline structures keep the same below $T_{\rm M}$, the peak shift of (004) toward smaller $d$ indicates that the lattice parameter $c$ also decreases. The lattice parameter $c$ in Fig. 3(b) obtained from OSIRIS diffractometer is slightly larger than that in Table 1 obtained from WOMBAT diffractometer, which are mainly attributed to the difference between the two diffractometers. The order parameter of the sinusoidal magnetism can be represented by the normalized intensities of two magnetic peaks (101)$_{\rm M}-k$ and (000)$_{\rm M} \pm k$, which are plotted together with the lattice constant $c$ in Fig. 3(b) for comparison. Surprisingly, all these parameters decrease simultaneously in a uniform manner with increasing temperature until a kink occurs at 170 K, in perfect agreement with the transition temperature reported previously.[12,13] The analogous temperature-dependent behavior in the wide temperature range from 10 K to 250 K for the normalized intensity of magnetic peaks and lattice constant $c$ suggests a strong coupling between the spin and lattice (“magneto-elastic” coupling) in Cr$_2$GaN. This is extremely alike the typical characteristics of Mn-based MAX material Mn$_2$CaC and MnNiGe, where the magnetostriction effect is accompanied with the coupling among spin, lattice and electrical transport properties.[7,8,17]
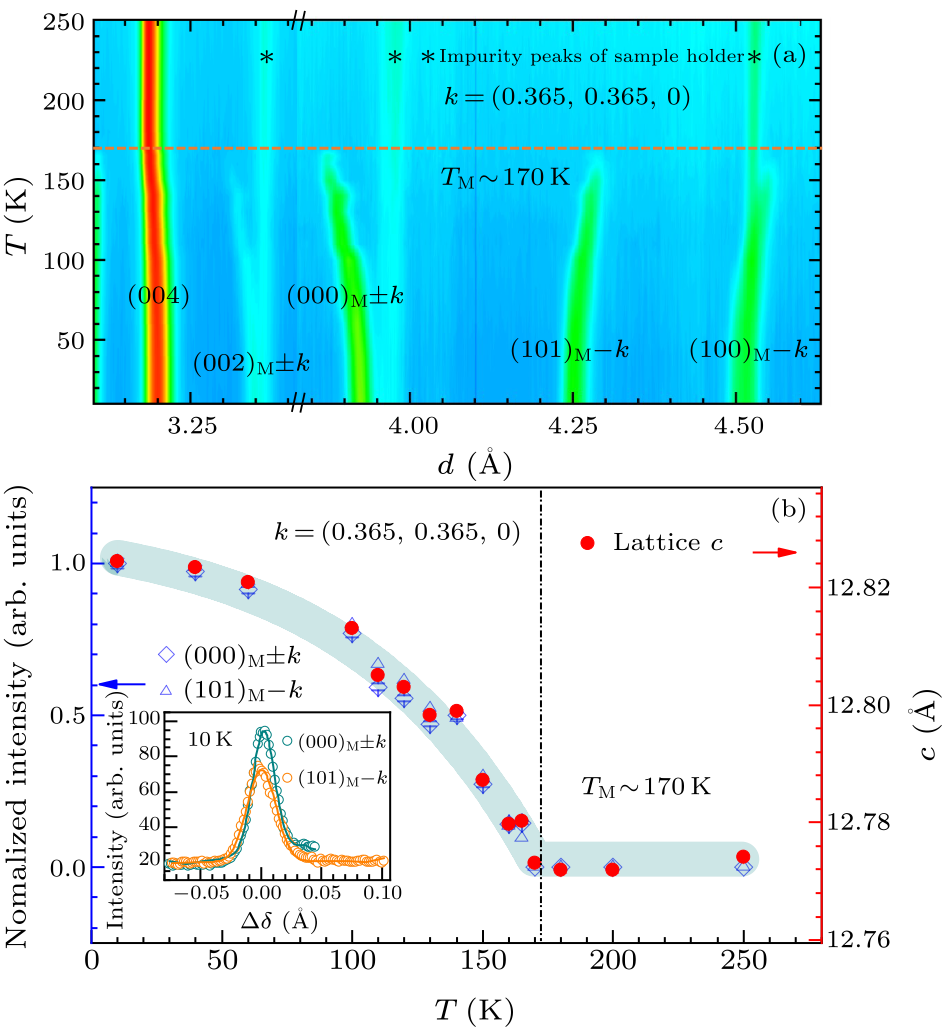
cpl-39-9-097501-fig3.png
Fig. 3. (a) The temperature-dependent nuclear peak (004) and magnetic peaks of (002)$_{\rm M} \pm k$, (000)$_{\rm M} \pm k$, (101)$_{\rm M}-k$, and (100)$_{\rm M}-k$. (b) Temperature dependence of the normalized intensity of magnetic peaks (000)$_{\rm M} \pm k$ and (101)$_{\rm M}-k$ and lattice constant $c$. The inset in Fig. 3(b) is the fitting of magnetic peaks at 10 K. For these magnetic peaks, the fits to Gauss function are performed for different temperatures, and the obtained area represent their intensity of magnetic peaks.
Recent research has suggested the potential for the practical application of the MAX phases. The challenges in the immediate future are to further explore and characterize the MAX phases reported so far and to make further advance in boosting their industrial application. Here, the presented experimental results show that Cr$_2$GaN exhibits a magnetic transition at 170 K, below which all Cr atoms are aligned with sinusoidal modulated magnetic structure. Accompanied with this magnetic transition, drastic change in the crystal structure of the material takes place, where 0.4% contraction in the out-of-plane $c$ axis with increasing temperature from 10 K to 170 K indicates that it is a considerably large effect compared to what has commonly been observed in magnetostriction systems. The reported magneto-elastic coupling in Cr$_2$GaN is much like that in Mn-based MAX phase Mn$_2$GaC, in which the anisotropic structural changes are argued to be driven by magnetism.[8] For Cr$_2$GaN, by simply stretching the lattice in the $c$ direction, the Cr–Cr interlayer distance is altered and thereby weakening magnetic coupling across the Ga layer, thus it becomes available to be capable of shifting the occurrence of magnetic transitions, as reported by doping and pressure effects in this compound.[12] Due to the magneto-elastic coupling interaction, it would be interesting for further studies to explore possible anisotropic response of the lattice and electrical conductivity to magnetic fields applied parallel and perpendicular to the $c$ axis. Therefore, the single crystals of Cr$_2$GaN are highly desired for transport experiments to explore possible magnetoelectric or magnetocaloric applications. Moreover, Cr$_2$GaN may be a candidate for topological magnetic texture or electronic states under its complex and tunable magnetism. To date, many novel magnetic topological materials, such as Co$_2$MnGa,[18-20] Co$_2$MnAl,[21,22] Co$_2$Ti$X$ ($X$ = Si, Ge and Sn),[23] $X$Co$_2 Z$ ($X$ = IVB or VB; $Z$ = IVA or IIIA),[24] Co$_3$Sn$_2$S$_2$,[25,26] and SrRuO$_3$,[27,28] have been identified by combining topology of electronic band structures with magnetic configurations. These novel materials exhibit rich topological states due to strong spin-orbit coupling or magneto-elastic coupling, referred such as magnetic topological insulators, Weyl and Dirac magnetic semimetals, axionic insulators or higher-order topological phases of matter.[29-36] For Cr$_2$GaN as a 211-type compound similar to those Co-based systems, if the topological states exist, it will be very interesting to tune the topological states by its crystal structure continuously regulated by magnetism upon decreasing temperature. In conclusion, the neutron powder diffraction and Rietveld refinement are carried out to determine the magnetic structure of Cr$_2$GaN, which is described as an incommensurate sinusoidal modulated structure with propagating vector $k = (0.365, 0.365, 0)$. Temperature-dependent diffraction patterns manifest that no structural transition occurs, but a $c$-axis lattice stretching below the magnetic phase transition temperature $T_{\rm M}\approx 170$ K, which shows a similar behavior with the magnetic order parameter. The reported magneto-elastic coupling interplay in Cr$_2$GaN will provide us a platform for further exploring the possible magnetoelectric, magnetostrictive, magnetocaloric effects and magnetic topological states in the MAX compounds. Acknowledgments. This work was supported by the National Natural Science Foundation of China (Grant Nos. 11822411, 12061130200, 11961160699, 11974392, and 52101236), the National Key Research and Development Program of China (Grant Nos. 2018YFA0704200, 2017YFA0303100, and 2020YFA0406003), the Strategic Priority Research Program (B) of the CAS (Grant No. XDB25000000), K. C. Wong Education Foundation (Grant No. GJTD-2020-01), the Youth Innovation Promotion Association of the CAS (Grant No. Y202001), Beijing Natural Science Foundation (Grant No. JQ19002), and the Newton Advanced Fellowship funding from the Royal Society of UK (Grant No. NAF$\backslash$R1$\backslash$201248). This work is based on neutron diffraction experiments performed at OSIRIS (Proposal No. RB1610019), ISIS Facility, Rutherford Appleton Laboratory, UK and WOMBAT (Proposal No. P6014), Australian Centre for Neutron Scattering, Australian Nuclear Science and Technology Organisation, Australia. References The MN+1AXN phases: A new class of solidsThe M+1AX phases: Materials science and thin-film processingProgress in research and development on MAX phases: a family of layered ternary compoundsThe MAX Phases: Unique New Carbide and Nitride MaterialsSynthesis and Characterization of a Remarkable Ceramic: Ti3SiC2Magnetic MAX phases from theory and experiments; a reviewLarge uniaxial magnetostriction with sign inversion at the first order phase transition in the nanolaminated Mn2GaC MAX phaseMagnetically driven anisotropic structural changes in the atomic laminate M n 2 GaC Magnetic properties of bulk and thin film Cr–Al–C compoundsMagnetic Anisotropy in the (Cr0.5 Mn0.5 )2 GaC MAX PhaseMn-doping-induced itinerant-electron ferromagnetism in Cr 2 GeCSuppression of a possible spin-density wave transition in Cr2 GaN by Ge dopingMagnetic ground state of the M n + 1 A X n -phase nitride Cr 2 GaNA profile refinement method for nuclear and magnetic structuresRecent advances in magnetic structure determination by neutron powder diffractionA new protocol for the determination of magnetic structures using simulated annealing and representational analysis (SARAh)Magnetic and Structural Transitions Tuned through Valence Electron Concentration in Magnetocaloric Mn(Co 1– x Ni x )GeGiant anomalous Nernst effect and quantum-critical scaling in a ferromagnetic semimetalFrom Colossal to Zero: Controlling the Anomalous Hall Effect in Magnetic Heusler Compounds via Berry Curvature DesignAnomalous Nernst effect beyond the magnetization scaling relation in the ferromagnetic Heusler compound Co2MnGaExploring Co2 MnAl Heusler compound for anomalous Hall effect sensorsGiant room temperature anomalous Hall effect and tunable topology in a ferromagnetic topological semimetal Co2MnAlRoom-temperature magnetic topological Weyl fermion and nodal line semimetal states in half-metallic Heusler Co2TiX (X=Si, Ge, or Sn)Time-Reversal-Breaking Weyl Fermions in Magnetic Heusler AlloysSpin excitations and spin wave gap in the ferromagnetic Weyl semimetal Co3Sn2S2Anisotropic magnetoelastic response in the magnetic Weyl semimetal Co3Sn2S2Weyl fermions and spin dynamics of metallic ferromagnet SrRuO3Interplay of Electronic and Spin Degrees in Ferromagnetic SrRuO 3 : Anomalous Softening of the Magnon Gap and StiffnessHigh-throughput calculations of magnetic topological materialsIntrinsic magnetic topological insulatorsProgress and prospects in magnetic topological materialsInvestigation of point-contact Andreev reflection on magnetic Weyl semimetal Co3Sn2S2Spin waves in magnetic Weyl semimetalsWeyl monopoles dance with the spin wavesTopological magnon insulator spin excitations in the two-dimensional ferromagnet CrBr 3 Nature of spin-lattice coupling in two-dimensional CrI3 and CrGeTe3
[1] Barsoum M W 2000 Prog. Solid State Chem. 28 201
[2] Eklund P et al. 2010 Thin Solid Films 518 1851
[3] Sun Z M 2011 Int. Mater. Rev. 56 143
[4] Barsoum M W et al. 2001 Am. Sci. 89 334
[5] Barsoum M W et al. 1996 J. Am. Ceram. Soc. 79 1953
[6] Ingason A S, Dahlqvist M, and Rosen J 2016 J. Phys.: Condens. Matter 28 433003
[7] Novoselova I P et al. 2018 Sci. Rep. 8 2637
[8] Dahlqvist M et al. 2016 Phys. Rev. B 93 014410
[9] Boucher R, Berger O, and Leyens C 2016 Surf. Eng. 32 172
[10] Salikhov R et al. 2015 Mater. Res. Lett. 3 156
[11] Liu Z, Waki T, Tabata Y, and Nakamura H 2014 Phys. Rev. B 89 054435
[12] Li Y F, Liu J Z, Liu W H, Zhu X Y, and Wen H H 2015 Philos. Mag. 95 2831
[13] Liu Z, Waki T, Tabata Y, Yuge K, Nakamura H, and Watanabe I 2013 Phys. Rev. B 88 134401
[14] Rietveld H M 1969 J. Appl. Crystallogr. 2 65
[15] Rodríguez-Carvajal J 1993 Phys. B: Condens. Matter 192 55
[16] Wills A S 2000 Physica B 276–278 680
[17] Ren Q Y, Hutchison W D, Wang J L, Studer A J, and Campbell S J 2018 Chem. Mater. 30 1324
[18] Akito S et al. 2018 Nat. Phys. 14 1119
[19] Manna K et al. 2018 Phys. Rev. X 8 041045
[20] Guin S N et al. 2019 NPG Asia Mater. 11 16
[21] Vilanova V E, Stryganyuk G, Schneider H, Felser C, and Jakob G 2011 Appl. Phys. Lett. 99 132509
[22] Li P G et al. 2020 Nat. Commun. 11 3476
[23] Chang G Q et al. 2016 Sci. Rep. 6 38839
[24] Wang Z J et al. 2016 Phys. Rev. Lett. 117 236401
[25] Liu C et al. 2021 Sci. Chin. Phys. Mech. & Astron. 64 217062
[26] Liu C et al. 2021 Sci. Chin. Phys. Mech. & Astron. 64 257511
[27] Itoh S et al. 2016 Nat. Commun. 7 11788
[28] Jenni K et al. 2019 Phys. Rev. Lett. 123 017202
[29] Xu Y F et al. 2020 Nature 586 702
[30] Wang P Y, Ge J, Li J H, Liu Y Z, Xu Y, and Wang J 2021 Innovation 2 100098
[31] Bernevig B A, Felser C, and Beidenkopf H 2022 Nature 603 41
[32] Wang H et al. 2020 Sci. Chin. Phys. Mech. & Astron. 63 287411
[33] Xie X C 2021 Sci. Chin. Phys. Mech. & Astron. 64 217061
[34] Yan B H 2021 Sci. Chin. Phys. Mech. & Astron. 64 217063
[35] Cai Z W et al. 2020 Phys. Rev. B 104 L020402
[36] Li J, Feng J S, Wang P S, Kan E J, and Xiang H J 2021 Sci. Chin. Phys. Mech. & Astron. 64 286811