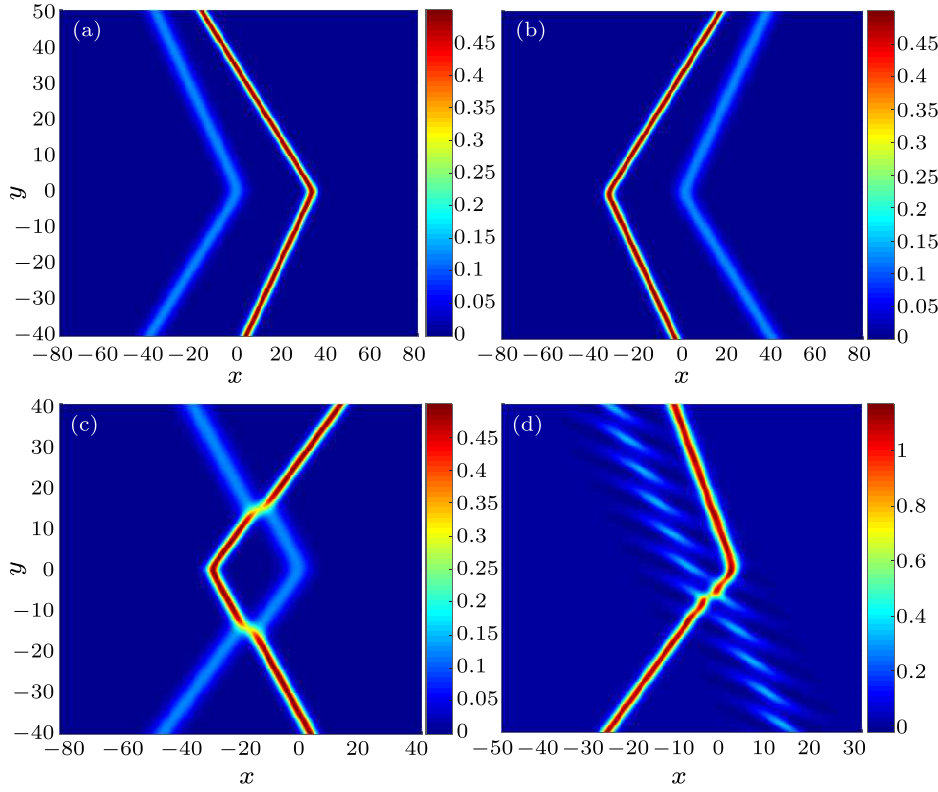
Fig. 3. Four different types of interactions at $t=0$: (a) interaction between a resonant soliton, and a resonant soliton as described by Eq. (13), where $k_{{1}}={1}$, $k_{{2}}={1}$, $k_{{3}}=\frac{1}{2}$, $k_{{4}}=\frac{1}{2}$, $p_{{1}}=\frac{6}{8}$, $p_{{2}}={1}$, $p_{{3}}=\frac{6}{16}$, $p_{{4}}={\frac{1}{2}}$, $\phi_{{1}}=-30$, $\phi_{{2}}=-30$, $\phi_{{3} }=0$, $\phi_{{4}}=0$; (b) interaction between a resonant soliton and a resonant soliton as described by Eq. (13), where $k_{{1}}={-1}$, $k_{{2}}={-1}$, $k_{{3}}=-\frac{1}{2}$, $k_{{4}}=-\frac{1}{2}$, $p_{{1}}=\frac{6}{8}$, $p_{{2}}={1}$, $p_{{3}}=\frac{6}{16}$, $p_{{4}}={\frac{1}{2}}$, $\phi_{{1}}=-30$, $\phi_{{2}}=-30$, $\phi_{{3} }=0$, $\phi_{{4}}=0$; (c) interaction between a resonant soliton and a resonant soliton, as described by Eq. (13), where $k_{{1}}={-1}$, $k_{{2}}={-1}$, $k_{{3}}=\frac{1}{2}$, $k_{{4}}=\frac{1}{2}$, $p_{{1}}=\frac{6}{8}$, $p_{{2}}={1}$, $p_{{3}}=\frac{6}{16}$, $p_{{4}}={\frac{1}{2}}$, $\phi_{{1}}=-30,\phi_{{2}}=-30$, $\phi_{{3} }=0$, $\phi_{{4}}=0$; (d) nonlinear superposition between a space-curved resonant line soliton and a breather wave, as described by Eq. (6), where $k_{{1}}=\frac{2}{7}+\frac{3}{7}i$, $k_{{2}}=\frac{2}{7}-\frac{3}{7}i$, $p_{{1}}=\frac{1}{8}+i$, $p_{{2}}=\frac{1}{8}-i$, $k_{{3}}=\frac{3}{2}$, $k _{{4}}=\frac{3}{2}$, $p_{{3}}=\frac{1}{2}$, $p_{{4}}={-1}$, $\phi_{{1}}=1$, $\phi_{{2}}=1$, $\phi_{{3}}=0$, $\phi_{{4}}=0$.