| GENERAL |
 |
|

|
|
|
Imaginary Time Crystal of Thermal Quantum Matter |
| Zi Cai1,2**, Yizhen Huang1, W. Vincent Liu3,4,2** |
1Wilczek Quantum Center and Key Laboratory of Artificial Structures and Quantum Control, School of Physics and Astronomy, Shanghai Jiao Tong University, Shanghai 200240
2Shanghai Research Center for Quantum Sciences, Shanghai 201315
3Department of Physics and Astronomy, University of Pittsburgh, Pittsburgh, Pennsylvania 15260, USA
4Wilczek Quantum Center, School of Physics and Astronomy and T. D. Lee Institute, Shanghai Jiao Tong University, Shanghai 200240
|
|
| Cite this article: |
|
Zi Cai, Yizhen Huang, W. Vincent Liu 2020 Chin. Phys. Lett. 37 050503 |
|
|
|
|
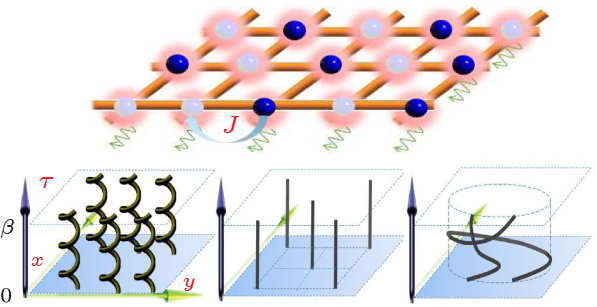
Abstract Temperature is a fundamental thermodynamic variable for matter. Physical observables are often found to either increase or decrease with it, or show a non-monotonic dependence with peaks signaling underlying phase transitions or anomalies. Statistical field theory has established connection between temperature and time: a quantum ensemble with inverse temperature $\beta$ is formally equivalent to a dynamic system evolving along an imaginary time from 0 to $i\beta$ in the space one dimension higher. Here we report that a gas of hard-core bosons interacting with a thermal bath manifests an unexpected temperature-periodic oscillation of its macroscopic observables, arising from the microscopic origin of space-time locked translational symmetry breaking and crystalline ordering. Such a temperature crystal, supported by quantum Monte Carlo simulation, generalizes the concept of purely spatial density-wave order to the imaginary time axis for Euclidean action.
|
|
Received: 08 April 2020
Published: 25 April 2020
|
|
| PACS: |
05.30.Jp
|
(Boson systems)
|
| |
02.70.Ss
|
(Quantum Monte Carlo methods)
|
| |
03.65.Yz
|
(Decoherence; open systems; quantum statistical methods)
|
|
|
| Fund: Supported in part by the National Key Research and Development Program of China (Grant No. 2016YFA0302001), the National Natural Science Foundation of China (Grant Nos. 11674221 and 11745006), the Shanghai Rising-Star Program, Eastern Scholar Professor of Distinguished Appointment Program, the AFOSR (Grant No. FA9550-16-1-0006), the MURI-ARO (Grant No. W911NF-17-1-0323) through UC Santa Barbara, the NSF China Overseas Scholar Collaborative Program (Grant No. 11429402), and the Shanghai Municipal Science and Technology Major Project (Grant No. 2019SHZDZX01). |
|
|
|
| [1] | Wilczek F 2012 Phys. Rev. Lett. 109 160401 | | [2] | Shapere A and Wilczek F 2012 Phys. Rev. Lett. 109 160402 | | [3] | Li T, Gong Z X, Yin Z Q, Quan H T, Yin X, Zhang P, Duan L M and Zhang X 2012 Phys. Rev. Lett. 109 163001 | | [4] | Wilczek F 2013 Phys. Rev. Lett. 111 250402 | | [5] | Sacha K 2015 Phys. Rev. A 91 033617 | | [6] | Else D V, Bauer B and Nayak C 2016 Phys. Rev. Lett. 117 090402 | | [7] | Khemani V, Lazarides A, Moessner R and Sondhi S L 2016 Phys. Rev. Lett. 116 250401 | | [8] | Yao N Y, Potter A C, Potirniche I D and Vishwanath A 2017 Phys. Rev. Lett. 118 030401 | | [9] | Syrwid A, Zakrzewski J and Sacha K 2017 Phys. Rev. Lett. 119 250602 | | [10] | Khemani V, von Keyserlingk C W and Sondhi S L 2017 Phys. Rev. B 96 115127 | | [11] | Russomanno A, Iemini F, Dalmonte M and Fazio R 2017 Phys. Rev. B 95 214307 | | [12] | Gong Z, Hamazaki R and Ueda M 2018 Phys. Rev. Lett. 120 040404 | | [13] | Huang B, Wu Y H and Liu W V 2018 Phys. Rev. Lett. 120 110603 | | [14] | Sacha K and Zakrzewski J 2018 Rep. Prog. Phys. 81 016401 | | [15] | Iemini F, Russomanno A, Keeling J, Schirò M, Dalmonte M and Fazio R 2018 Phys. Rev. Lett. 121 035301 | | [16] | Kozin V K and Kyriienko O 2019 Phys. Rev. Lett. 123 210602 | | [17] | Chew A, Mross D F and Alicea J 2019 arXiv:1907.12570 | | [18] | Bruno P 2013 Phys. Rev. Lett. 111 070402 | | [19] | Watanabe H and Oshikawa M 2015 Phys. Rev. Lett. 114 251603 | | [20] | Choi S, Landig R, Kucsko G, Zhou H, Isoya J, Jelezko F, Onoda S, Sumiya H, Khemani V, von Keyserlingk C 2017 Nature 543 221 | | [21] | Zhang J, Hess P W, Kyprianidis A, Becker P, Lee A, Smith J, Pagano G, Potirniche I D, Potter A C, Vishwanath A 2017 Nature 543 217 | | [22] | Ruderman M A and Kittel C 1954 Phys. Rev. 96 99 | | [23] | Kasuya T 1956 Prog. Theor. Phys. 16 45 | | [24] | Yosida K 1957 Phys. Rev. 106 893 | | [25] | Kozii V and Fu L 2017 arXiv:1708.05841 | | [26] | Cai Z, Schollwöck U and Pollet L 2014 Phys. Rev. Lett. 113 260403 | | [27] | Prokof'ev N V, Svistunov B V and Tupitsyn I S 1998 Phys. Lett. A 238 253 | | [28] | Mukhin S 2009 J. Supercond. Novel Magn. 22 75 | | [29] | Galitski V 2010 Phys. Rev. B 82 054511 | | [30] | DeSalvo B, Patel K, Cai G and Chin C 2019 Nature 568 61 |
|
|
Viewed |
|
|
|
Full text
|
|
|
|
|
Abstract
|
|
|
|
|